题目内容
8.已知二次函数y=-(x-1)2+5,当m≤x≤n且mn<0时,y的最小值为2m,最大值为2n,求m+n的值.分析 结合二次函数图象的开口方向、对称轴以及增减性进行解答即可.
解答 解:二次函数y=-(x-1)2+5的大致图象如下: .
.
①当m≤0≤x≤n<1时,当x=m时y取最小值,即2m=-(m-1)2+5,
解得:m=-2.
当x=n时y取最大值,即2n=-(n-1)2+5,
解得:n=2或n=-2(均不合题意,舍去);
②当m≤0≤x≤1≤n时,当x=m时y取最小值,即2m=-(m-1)2+5,
解得:m=-2.
当x=1时y取最大值,即2n=-(1-1)2+5,
解得:n=$\frac{5}{2}$,
所以m+n=-2+$\frac{5}{2}$=$\frac{1}{2}$.
点评 本题考查了二次函数的最值问题,二次函数的增减性,根据函数解析式求出对称轴解析式是解题的关键.

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目
19.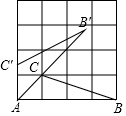 如图,点A、B、C均在边长为1的正方形网格的格点上,将△ABC绕着点A逆时针方向旋转得到△AB′C′,若使AB′经过点C,则$\widehat{B′B}$的长为( )
如图,点A、B、C均在边长为1的正方形网格的格点上,将△ABC绕着点A逆时针方向旋转得到△AB′C′,若使AB′经过点C,则$\widehat{B′B}$的长为( )
 如图,点A、B、C均在边长为1的正方形网格的格点上,将△ABC绕着点A逆时针方向旋转得到△AB′C′,若使AB′经过点C,则$\widehat{B′B}$的长为( )
如图,点A、B、C均在边长为1的正方形网格的格点上,将△ABC绕着点A逆时针方向旋转得到△AB′C′,若使AB′经过点C,则$\widehat{B′B}$的长为( )| A. | $\frac{π}{2}$ | B. | π | C. | 6π | D. | 7π |
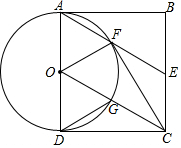 如图,正方形ABCD,E为BC边的中点,连接AE、OC,以AD为直径的⊙O交AE于点F,交OC于点G,连接CF,DG.
如图,正方形ABCD,E为BC边的中点,连接AE、OC,以AD为直径的⊙O交AE于点F,交OC于点G,连接CF,DG.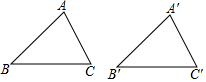 ①已知AB=A′B′,BC=B′C′,那只要再知道∠B=∠B′,就可以根据“SAS”得到△ABC≌△A′B′C′.
①已知AB=A′B′,BC=B′C′,那只要再知道∠B=∠B′,就可以根据“SAS”得到△ABC≌△A′B′C′.