题目内容
10.已知点A(a-1,5)和点B(2,b-1)关于x轴成轴对称,则(a+b)2016=1.分析 根据“关于x轴对称的点,横坐标相同,纵坐标互为相反数”列方程求出a、b的值,然后代入代数式进行计算即可得解.
解答 解:∵点A(a-1,5)和点B(2,b-1)关于x轴成轴对称,
∴a-1=2,b-1=-5,
解得a=3,b=-4,
所以,(a+b)2016=(3-4)2016=1.
故答案为:1.
点评 本题考查了关于x轴、y轴对称的点的坐标,解决本题的关键是掌握好对称点的坐标规律:(1)关于x轴对称的点,横坐标相同,纵坐标互为相反数;(2)关于y轴对称的点,纵坐标相同,横坐标互为相反数.

练习册系列答案
相关题目
20.下面“去分母”后所得方程正确的是( )
| A. | $\frac{x-3}{{x}^{2}-x}$+$\frac{2}{x-1}$=1,去分母,得x-3+2x=1 | |
| B. | $\frac{x-3}{{x}^{2}-x}$+$\frac{2}{x-1}$=1,去分母,得x-3+2=x2-x | |
| C. | $\frac{x-3}{{x}^{2}-x}$+$\frac{2}{x-1}$=1,去分母,得x-3+2x=x2-x | |
| D. | $\frac{x-3}{{x}^{2}-x}$+$\frac{2}{x-1}$=1,去分母,得x(x-3)+2x=x-1 |
18.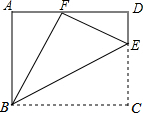 如图,矩形ABCD中,点E是CD边长的一点,△BCE沿BE折叠为△BFE,点F在AD上.
如图,矩形ABCD中,点E是CD边长的一点,△BCE沿BE折叠为△BFE,点F在AD上.
(1)求证:△ABF∽△DFE;
(2)若sin∠DFE=$\frac{1}{3}$,求tan∠FBE的值.
 如图,矩形ABCD中,点E是CD边长的一点,△BCE沿BE折叠为△BFE,点F在AD上.
如图,矩形ABCD中,点E是CD边长的一点,△BCE沿BE折叠为△BFE,点F在AD上.(1)求证:△ABF∽△DFE;
(2)若sin∠DFE=$\frac{1}{3}$,求tan∠FBE的值.
5. 如图,用尺规作图“过点C作CN∥OA”的实质就是作∠DOM=∠NCE,其作图依据是( )
如图,用尺规作图“过点C作CN∥OA”的实质就是作∠DOM=∠NCE,其作图依据是( )
 如图,用尺规作图“过点C作CN∥OA”的实质就是作∠DOM=∠NCE,其作图依据是( )
如图,用尺规作图“过点C作CN∥OA”的实质就是作∠DOM=∠NCE,其作图依据是( )| A. | SAS | B. | SSS | C. | ASA | D. | AAS |
2.为了了解某县七年级学生的体重情况,从中抽取了200名学生进行体重测试,就这个问题,下面说法正确的是( )
| A. | 200名学生是总体 | B. | 200名学生是一个样本 | ||
| C. | 每个学生是个体 | D. | 全县七年级学生的体重是总体 |
19.用代数式表示:“x的5倍与y的和的一半”可以表示为( )
| A. | 5x+$\frac{1}{2}$y | B. | $\frac{1}{2}$ (5x+y) | C. | $\frac{1}{2}$(5x+2y) | D. | 5x+y. |
 如图,一次函数y=ax+b的图象与反比例函数的图象交于A(-4,2),B(2,n)两点,且与x轴交于点C.
如图,一次函数y=ax+b的图象与反比例函数的图象交于A(-4,2),B(2,n)两点,且与x轴交于点C.



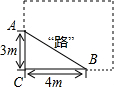 如图,某学校有一块长方形花圃,有极少数人为了避开拐角走“捷径”,在花圃内走出了一条“路”AB,爱心小组想在A处树立一个标牌“少走■米,踏之何刃?”请你计算后帮她们在标牌的■填上适当的数字为2米.
如图,某学校有一块长方形花圃,有极少数人为了避开拐角走“捷径”,在花圃内走出了一条“路”AB,爱心小组想在A处树立一个标牌“少走■米,踏之何刃?”请你计算后帮她们在标牌的■填上适当的数字为2米.