题目内容
18.计算:(1)|$\sqrt{6}$-3|-($\frac{1}{3}$)-1+$\sqrt{24}$
(2)先化简,再求值:($\frac{2a}{5{a}^{2}b}$+$\frac{3b}{10a{b}^{2}}$)÷$\frac{7}{2{a}^{3}{b}^{2}}$,其中a=$\frac{\sqrt{5}}{2}$,b=-$\frac{1}{2}$.
分析 (1)根据绝对值、负整数指数幂以及二次根式的化简进行计算即可;
(2)根据运算顺序,先算括号里面的,再算除法,最后把a,b的值代入计算即可.
解答 解:(1)原式=3-$\sqrt{6}$-3+2$\sqrt{6}$
=$\sqrt{6}$;
(2)原式=($\frac{2}{5ab}$+$\frac{3}{10ab}$)÷$\frac{7}{2{a}^{3}{b}^{2}}$,
=$\frac{7}{10ab}$•$\frac{2{a}^{3}{b}^{2}}{7}$
=$\frac{{a}^{2}b}{5}$,
当a=$\frac{\sqrt{5}}{2}$,b=-$\frac{1}{2}$时,原式=-$\frac{1}{8}$.
点评 本题考查了分式的化简求值、实数的运算以及负整数指数幂,熟练掌握运算顺序是解题的关键.

练习册系列答案
相关题目
3.学校准备从甲乙两位选手中选择一位选手代表学校参加所在地区的汉字听写大赛,学校对两位选手从表达能力、阅读理解、综合素质和汉字听写四个方面做了测试,他们各自的成绩(百分制)如表:
(1)由表中成绩已算得甲的平均成绩为80.25,请计算乙的平均成绩,从他们的这一成绩看,应选派谁;
(2)如果表达能力、阅读理解、综合素质和汉字听写分别赋予它们2、1、3和4的权,请分别计算两名选手的平均成绩,从他们的这一成绩看,应选派谁.
| 选手 | 表达能力 | 阅读理解 | 综合素质 | 汉字听写 |
| 甲 | 85 | 78 | 85 | 73 |
| 乙 | 73 | 80 | 82 | 83 |
(2)如果表达能力、阅读理解、综合素质和汉字听写分别赋予它们2、1、3和4的权,请分别计算两名选手的平均成绩,从他们的这一成绩看,应选派谁.
10. 如图A,B,C是⊙O上的三个点,若∠AOC=100°,则∠ABC等于( )
如图A,B,C是⊙O上的三个点,若∠AOC=100°,则∠ABC等于( )
 如图A,B,C是⊙O上的三个点,若∠AOC=100°,则∠ABC等于( )
如图A,B,C是⊙O上的三个点,若∠AOC=100°,则∠ABC等于( )| A. | 50° | B. | 80° | C. | 100° | D. | 130° |
2.某校将举行一场“汉字电脑录入大赛”,要求各班推选一名同学参加比赛.为此,初三(1)班组织了五轮班级选拔赛,在这五轮选拔赛中,甲、乙两位同学的平均分都是95分,甲的成绩的方差是0.3,乙的成绩的方差是0.7,根据以上数据,下列说法正确的是( )
| A. | 甲的成绩比乙的成绩稳定 | B. | 乙的成绩比甲的成绩稳定 | ||
| C. | 甲、乙两人的成绩一样稳定 | D. | 无法确定甲、乙的成绩谁更稳定 |
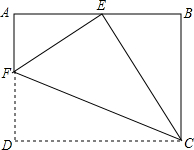 如图,将一张矩形纸片ABCD沿CF折叠,使点D与AB的中点E重合,求$\frac{AF}{FD}$.
如图,将一张矩形纸片ABCD沿CF折叠,使点D与AB的中点E重合,求$\frac{AF}{FD}$.