题目内容
1.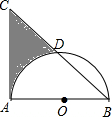 如图,等腰直角△ABC中,AB=AC=8,以AB为直径的半圆O交斜边BC于D,则阴影部分面积为(结果保留π)( )
如图,等腰直角△ABC中,AB=AC=8,以AB为直径的半圆O交斜边BC于D,则阴影部分面积为(结果保留π)( )| A. | 24-4π | B. | 32-4π | C. | 32-8π | D. | 16 |
分析 连接AD,因为△ABC是等腰直角三角形,故∠ABD=45°,再由AB是圆的直径得出∠ADB=90°,故△ABD也是等腰直角三角形,所以$\widehat{AD}$=$\widehat{BD}$,S阴影=S△ABC-S△ABD-S弓形AD由此可得出结论.
解答 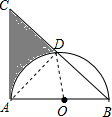 解:连接AD,OD,
解:连接AD,OD,
∵等腰直角△ABC中,
∴∠ABD=45°.
∵AB是圆的直径,
∴∠ADB=90°,
∴△ABD也是等腰直角三角形,
∴$\widehat{AD}$=$\widehat{BD}$.
∵AB=8,
∴AD=BD=4$\sqrt{2}$,
∴S阴影=S△ABC-S△ABD-S弓形AD=S△ABC-S△ABD-(S扇形AOD
-$\frac{1}{2}$S△ABD)=$\frac{1}{2}$×8×8-$\frac{1}{2}$×4$\sqrt{2}$×4$\sqrt{2}$-$\frac{90π×{4}^{2}}{360}$+$\frac{1}{2}$×$\frac{1}{2}$×4$\sqrt{2}$×4$\sqrt{2}$=16-4π+8=24-4π.
故选A.
点评 本题考查的是扇形面积的计算,熟记扇形的面积公式是解答此题的关键.

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目
12. 如图,PA和PB是⊙O的切线,点A和点B是切点,AC是⊙O的直径,已知∠P=40°,则∠ACB的大小是( )
如图,PA和PB是⊙O的切线,点A和点B是切点,AC是⊙O的直径,已知∠P=40°,则∠ACB的大小是( )
 如图,PA和PB是⊙O的切线,点A和点B是切点,AC是⊙O的直径,已知∠P=40°,则∠ACB的大小是( )
如图,PA和PB是⊙O的切线,点A和点B是切点,AC是⊙O的直径,已知∠P=40°,则∠ACB的大小是( )| A. | 40° | B. | 60° | C. | 70° | D. | 80° |
16.计算(-a3)2的结果是( )
| A. | a5 | B. | -a5 | C. | a6 | D. | -a6 |
10. 如图A,B,C是⊙O上的三个点,若∠AOC=100°,则∠ABC等于( )
如图A,B,C是⊙O上的三个点,若∠AOC=100°,则∠ABC等于( )
 如图A,B,C是⊙O上的三个点,若∠AOC=100°,则∠ABC等于( )
如图A,B,C是⊙O上的三个点,若∠AOC=100°,则∠ABC等于( )| A. | 50° | B. | 80° | C. | 100° | D. | 130° |
 已知抛物线y=x2+2x-3与x轴交于A,B(点A在点B的左侧)两单,与y轴交于点C.
已知抛物线y=x2+2x-3与x轴交于A,B(点A在点B的左侧)两单,与y轴交于点C. 如图,某仓储中心有一斜坡AB,其坡度为i=1:2,顶部A处的高AC为4m,B、C在同一水平地面上.
如图,某仓储中心有一斜坡AB,其坡度为i=1:2,顶部A处的高AC为4m,B、C在同一水平地面上.