题目内容
已知抛物线y=
(x-1)2-3.
(1)写出抛物线的开口方向、对称轴;
(2)函数y有最大值还是最小值?并求出这个最大(小)值;
(3)设抛物线与y轴的交点为P,与x轴的交点为Q,求P、Q两点坐标.
| 3 |
| 4 |
(1)写出抛物线的开口方向、对称轴;
(2)函数y有最大值还是最小值?并求出这个最大(小)值;
(3)设抛物线与y轴的交点为P,与x轴的交点为Q,求P、Q两点坐标.
考点:二次函数的性质,二次函数的最值
专题:
分析:(1)根据二次函数的性质,写出开口方向与对称轴即可;
(2)根据a是正数确定有最小值,再根据函数解析式写出最小值;
(3)将x=0代入y=
(x-1)2-3,求出y的值,得到点P的坐标;将y=0代入y=
(x-1)2-3,解方程求出x的值,得到点Q的坐标.
(2)根据a是正数确定有最小值,再根据函数解析式写出最小值;
(3)将x=0代入y=
| 3 |
| 4 |
| 3 |
| 4 |
解答:解:(1)抛物线y=
(x-1)2-3,
∵a=
>0,
∴抛物线的开口向上,
对称轴为直线x=1;
(2)∵a=
>0,
∴函数y有最小值,最小值为-3;
(3)令x=0,则y=
(0-1)2-3=-
,
所以,点P的坐标为(0,-
),
令y=0,则
(x-1)2-3=0,
解得x1=-1,x2=3,
所以,点Q的坐标为(-1,0)或(3,0).
| 3 |
| 4 |
∵a=
| 3 |
| 4 |
∴抛物线的开口向上,
对称轴为直线x=1;
(2)∵a=
| 3 |
| 4 |
∴函数y有最小值,最小值为-3;
(3)令x=0,则y=
| 3 |
| 4 |
| 9 |
| 4 |
所以,点P的坐标为(0,-
| 9 |
| 4 |
令y=0,则
| 3 |
| 4 |
解得x1=-1,x2=3,
所以,点Q的坐标为(-1,0)或(3,0).
点评:本题主要考查了二次函数的性质,二次函数的最值问题,以及抛物线与坐标轴的交点问题,是基础题,熟记二次函数的开口方向,对称轴解析式与二次函数的系数的关系是解题的关键.

练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
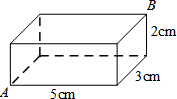 如图,已知长方体的长、宽、高分别是5cm、3cm、2cm,一只蚂蚁要从长方体盒子的一个顶点A处,沿着长方体的表面到长方体和A相对的顶点B处吃食物,那么它需要爬行的最短路径的长是
如图,已知长方体的长、宽、高分别是5cm、3cm、2cm,一只蚂蚁要从长方体盒子的一个顶点A处,沿着长方体的表面到长方体和A相对的顶点B处吃食物,那么它需要爬行的最短路径的长是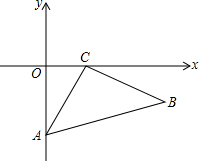 已知:在平面直角坐标系中,△ABC的顶点A、C分别在y轴、x轴上,且∠ACB=90°,AC=BC.如图,当A(0,-2),C(1,0),点B在第四象限时,则点B的坐标为:(
已知:在平面直角坐标系中,△ABC的顶点A、C分别在y轴、x轴上,且∠ACB=90°,AC=BC.如图,当A(0,-2),C(1,0),点B在第四象限时,则点B的坐标为:( 如图所示,△ABC是等边三角形,延长AC到D,以BD为边作等边△BDE,连接AE.
如图所示,△ABC是等边三角形,延长AC到D,以BD为边作等边△BDE,连接AE.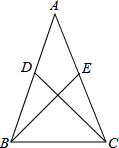 如图:△ABC中,点E和点D分别为AC、AB上的点,且BE=CD,AB=AC,求证:∠ABE=∠ACD.
如图:△ABC中,点E和点D分别为AC、AB上的点,且BE=CD,AB=AC,求证:∠ABE=∠ACD.