题目内容
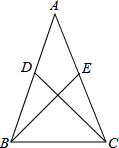 如图:△ABC中,点E和点D分别为AC、AB上的点,且BE=CD,AB=AC,求证:∠ABE=∠ACD.
如图:△ABC中,点E和点D分别为AC、AB上的点,且BE=CD,AB=AC,求证:∠ABE=∠ACD.考点:全等三角形的判定与性质
专题:证明题
分析:易证BD=CE,即可证明△BCE≌△CBD,可得∠CBE=∠BCD,根据AB=AC,即可解题.
解答:解:∵AB=AC,
∴∠ABC=∠ACB,
∵BE2=CE2+BC2-2BC•CEcos∠ACB,
CD2=BD2+BC2-2BC•BDcos∠ABC,BE=CD,
∴BD=CE,
在△BCE和△CBD中,
,
∴△BCE≌△CBD(SAS),
∴∠CBE=∠BCD,
∴∠ABE=∠ACD.
∴∠ABC=∠ACB,
∵BE2=CE2+BC2-2BC•CEcos∠ACB,
CD2=BD2+BC2-2BC•BDcos∠ABC,BE=CD,
∴BD=CE,
在△BCE和△CBD中,
|
∴△BCE≌△CBD(SAS),
∴∠CBE=∠BCD,
∴∠ABE=∠ACD.
点评:本题考查了全等三角形的判定,考查了全等三角形对应边相等的性质,本题中求证△BCE≌△CBD是解题的关键.

练习册系列答案
相关题目
已知在Rt△ABC中,∠C=90°,AC=3,BC=4,则tanA的值为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
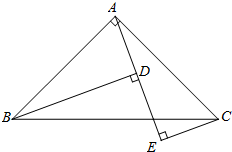 如图,已知△ABC中,∠BAC=90°,AB=AC,B、C在A、E的异侧,BD⊥AE于D,CE⊥AE于E.求证:
如图,已知△ABC中,∠BAC=90°,AB=AC,B、C在A、E的异侧,BD⊥AE于D,CE⊥AE于E.求证: 已知△PDC,A、B分別是PD和PC上一点,∠ABC=∠BCD,求证:PA•PD=PB•PC+AB•CD.
已知△PDC,A、B分別是PD和PC上一点,∠ABC=∠BCD,求证:PA•PD=PB•PC+AB•CD. 直线EF,CD相交于点O,OA⊥OB,且OC平分∠AOF,若∠AOF=140°,则∠BOD的度数为
直线EF,CD相交于点O,OA⊥OB,且OC平分∠AOF,若∠AOF=140°,则∠BOD的度数为 如图,若用(2,3)表示图上校门A的位置,则图书馆B的位置可表示为
如图,若用(2,3)表示图上校门A的位置,则图书馆B的位置可表示为