题目内容
9.在一张长为100cm,宽为80cm的矩形纸板ABCD地四个角,各剪去一个大小相同的正方形,做成一个无盖的盒子,图案设计如图所示.如果要使盒子的底面积比其剪去的面积多800cm2.(1)求盒子的高.
(2)有一根长为80cm的甘蔗能否放入此盒中?若能,请说明理由;若不能,请求出甘蔗露在盒子外面部分h(单位:cm)的取值范围.(不计甘蔗粗度)

分析 (1)根据题意表示出盒子的底面积,进而得出等式求出答案;
(2)根据题意结合勾股定理得出答案.
解答 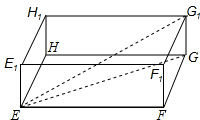 解:(1)设盒子的高为xcm,根据题意可得:
解:(1)设盒子的高为xcm,根据题意可得:
(100-2x)(80-2x)=4x2+800,
解得:x=20,
答:盒子的高为20cm;
(2)如图所示:由题意可得,EF=60,FG=40,
则EG=$\sqrt{6{0}^{2}+4{0}^{2}}$=$\sqrt{5200}$,
故EG1=$\sqrt{E{G}^{2}+2{0}^{2}}$=$\sqrt{5600}$<$\sqrt{8{0}^{2}}$,
∵$\sqrt{5600}$=20$\sqrt{14}$,
∴甘蔗露在盒子外面部分h(单位:cm)的取值范围为:80-20$\sqrt{14}$≤h≤20.
点评 此题主要考查了一元一次方程的应用以及勾股定理,正确表示出盒子底面积是解题关键.

练习册系列答案
相关题目
 如图,已知点(1,3)在函数y=$\frac{k}{x}$的图象上,矩形ABCD的边BC在x轴正半轴上,E是对角线BD的中点,函数y=$\frac{k}{x}$(x>0)的图象又经过A、E两点,点E的横坐标为m,解答下列问题:
如图,已知点(1,3)在函数y=$\frac{k}{x}$的图象上,矩形ABCD的边BC在x轴正半轴上,E是对角线BD的中点,函数y=$\frac{k}{x}$(x>0)的图象又经过A、E两点,点E的横坐标为m,解答下列问题: