题目内容
20．如果a，b，c的长度之和为32cm，且$\frac{a+b}{7}$=$\frac{b+c}{5}$=$\frac{a+c}{4}$，那么这三条线段能围成一个三角形吗？分析 设$\frac{a+b}{7}$=$\frac{b+c}{5}$=$\frac{a+c}{4}$=k，则a+b=7k，b+c=5k，a+c=4k，再根据a，b，c的长度之和为32cm可算出k的值，进而可得方程组$\left\{\begin{array}{l}{a+b=28}\\{b+c=20}\\{c+a=16}\end{array}\right.$，解方程组可得a、b、c的长，然后根据三角形的三边关系可得答案．
解答 解：设$\frac{a+b}{7}$=$\frac{b+c}{5}$=$\frac{a+c}{4}$=k，
则a+b=7k，b+c=5k，a+c=4k，
∴a+b+b+c+a+c=7k+5k+4k，
2（a+b+c）=16k，
a+b+c=8k，
∵a，b，c的长度之和为32cm，
∴8k=32，
k=4，
∴$\left\{\begin{array}{l}{a+b=28}\\{b+c=20}\\{c+a=16}\end{array}\right.$，
解得$\left\{\begin{array}{l}{a=12}\\{b=16}\\{c=4}\end{array}\right.$，
∵a+c=b，
∴这三条线段不能围成一个三角形．
点评 此题主要考查了三角形的三边关系，关键是正确求出a、b、c的长，掌握三角形两边之和大于第三边．
练习册系列答案
相关题目
5．为了鼓励市民节约用水，某市居民生活用水按阶梯式水价计费，表是该市居民“一户一表”生活用水阶梯式计费价格表的部分信息：
（说明：①每户产生的污水量等于该户的自来水用水量，②水费=自来水费用+污水处理费；
已知小王家2015年5月份用水20吨，交水费66元；6月份用水25吨，交水费91元．
（1）求a、b的值．
（2）随着夏天的到来，用水量将增加，为了节省开支，小王计划把7月份水费控制在不超过家庭月收入的2%，若小王家的月收入为9600元，则小王家7月份最多能用水多少吨？（结果精确到1吨）
| 自来水销售价格 | 污水处理价格 | |
| 每户每月用水量 | 单价：元/吨 | 单价：元/吨 |
| 17吨及以下 | a | 0.80 |
| 超过17吨但不超过30吨的部分 | b | 0.80 |
| 超过30吨的部分 | 6.00 | 0.80 |
已知小王家2015年5月份用水20吨，交水费66元；6月份用水25吨，交水费91元．
（1）求a、b的值．
（2）随着夏天的到来，用水量将增加，为了节省开支，小王计划把7月份水费控制在不超过家庭月收入的2%，若小王家的月收入为9600元，则小王家7月份最多能用水多少吨？（结果精确到1吨）
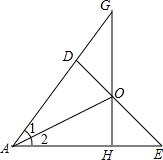已知：如图，OD⊥AD，OH⊥AE，DE交GH于O．