题目内容
9.阅读第(1)题的解答过程,再做第(2)题.(1)已知x+x-1=5,求x3+x-3的值.
解:∵x2+x-2
=(x+x-1)2-2
=52-2=23,
∴x3+x-3
=(x+x-1)(x2+x-2)-(x•x-2+x-1•x2)
=(x+x-1)(x2+x-2)-(x-1+x)
=5×23-5
=110.
(2)已知x+x-1=3,用两种方法求x5+x-5的值.
分析 方法一:根据(1)可得出x5+x-5=(x3+x-3)(x2+x-2)-(x+x-1),整体代入即可;
方法二:由x+x-1=3,利用完全平方公式可求出x2+x-2=7,再利用分式乘法可求出x3+x-3=18,也可求出x4+x-4=47,再利用分式乘法求出x5+x-5+x3+x-3=141,即可得出x5+x-5的值
解答 解:方法一:
∵x+x-1=3,
∴x2+x-2
=(x+x-1)2-2
=32-2=7,
∴x3+x-3
=(x+x-1)(x2+x-2)-(x•x-2+x-1•x2)
=(x+x-1)(x2+x-2)-(x-1+x)
=3×7-3
=18.
∴x5+x-5=(x3+x-3)(x2+x-2)-(x+x-1)
=18×7-3
=123.
方法二:
∵x+x-1=3,
∴(x+x-1)2=9,得x2+x-2=7,
∴(x+x-1)(x2+x-2)=21,化简得x3+x-3=18,
(x2+x-2)2=49,化简得x4+x-4=47,
(x+x-1)(x4+x-4)=3×47,化简得x5+x-5+x3+x-3=141,
∴x5+x-5=141-(x3+x-3)=141-18=123.
点评 本题考查了整式的混合运算,负整数指数幂,解题关键是整体代入的思想.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
1.半径为3的圆,如果半径增加2x,则面积S与x之间的函数表达式为( )
| A. | S=2π(x+3)2 | B. | S=9π+x | C. | S=4πx2+12x+9 | D. | S=4πx2+12πx+9π |
20.下列计算正确的是( )
| A. | 2$\sqrt{\frac{1}{2}}$=$\sqrt{2}$ | B. | $\sqrt{2}$$+\sqrt{3}$=$\sqrt{5}$ | C. | 4$\sqrt{3}$-3$\sqrt{3}$=1 | D. | 3+2$\sqrt{2}$=5$\sqrt{2}$ |
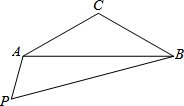 如图,已知等腰三角形ABC,∠ACB=120°且AC=BC=4,在平面内任作∠APB=60°,BP最大值为8.
如图,已知等腰三角形ABC,∠ACB=120°且AC=BC=4,在平面内任作∠APB=60°,BP最大值为8.