题目内容
19.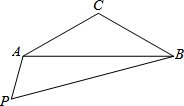 如图,已知等腰三角形ABC,∠ACB=120°且AC=BC=4,在平面内任作∠APB=60°,BP最大值为8.
如图,已知等腰三角形ABC,∠ACB=120°且AC=BC=4,在平面内任作∠APB=60°,BP最大值为8.
分析 先根据∠ACB=120°,∠APB=60°得出A、P、B、C四点共圆,故当PB是圆的直径时最长,此时∠PAB=90°,故∠ABP=30°,过点C作AB的垂线交PB于点O,则点O即为圆心,由等腰三角形的性质得出∠BCO=60°,∠ACB=30°.故可得出△OBC是等边三角形,由此可得出结论.
解答 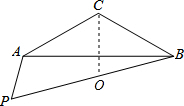 解:∵∠ACB=120°,∠APB=60°,
解:∵∠ACB=120°,∠APB=60°,
∴A、P、B、C四点共圆,
∴当PB是圆的直径时最长,
∴∠PAB=90°,
∴∠ABP=30°.
过点C作AB的垂线交PB于点O,则点O即为圆心,
∵∠ACB=120°且AC=BC=4,
∴∠BCO=60°,∠ACB=30°,
∴∠OBC=60°,
∴△OBC是等边三角形,
∴OC=BC=4,
∴PB=2OC=8.
故答案为:8.
点评 本题考查的是圆内接四边形的性质,熟知圆内接四边形的对角互补是解答此题的关键.

练习册系列答案
相关题目
14.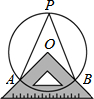 如图,将三角板的直角顶点放在⊙O的圆心上,两条直角边分别交⊙O于A,B两点,点P在优弧AB上,且与点A,B不重合,连结PA,PB,则∠APB度数是( )
如图,将三角板的直角顶点放在⊙O的圆心上,两条直角边分别交⊙O于A,B两点,点P在优弧AB上,且与点A,B不重合,连结PA,PB,则∠APB度数是( )
 如图,将三角板的直角顶点放在⊙O的圆心上,两条直角边分别交⊙O于A,B两点,点P在优弧AB上,且与点A,B不重合,连结PA,PB,则∠APB度数是( )
如图,将三角板的直角顶点放在⊙O的圆心上,两条直角边分别交⊙O于A,B两点,点P在优弧AB上,且与点A,B不重合,连结PA,PB,则∠APB度数是( )| A. | 20° | B. | 30° | C. | 45° | D. | 60° |
 如图,点B、C、D在同一直线上,AB=AD=CD,∠C=35°.求∠BAD的度数.
如图,点B、C、D在同一直线上,AB=AD=CD,∠C=35°.求∠BAD的度数.