题目内容
8.已知△ABC∽△DEF,其相似比为4:9,则△ABC与△DEF的面积比是( )| A. | 2:3 | B. | 3:2 | C. | 16:81 | D. | 81:16 |
分析 直接根据相似三角形的面积的比等于相似比的平方求解.
解答 解:∵△ABC∽△DEF,其相似比为4:9,
∴△ABC与△DEF的面积比是16:81.
故选C.
点评 本题考查了相似三角形的性质:相似三角形的对应角相等,对应边的比相等;相似三角形(多边形)的周长的比等于相似比;相似三角形的对应线段(对应中线、对应角平分线、对应边上的高)的比也等于相似比;相似三角形的面积的比等于相似比的平方.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
16.在-(-6),|-2|,-22,(-1)3,这四个数中,是负数的有( )
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
13. 如图,已知AB是⊙O的切线,点A为切点,连接OB交⊙O于点C,∠B=38°,点D是⊙O上一点,连接CD,AD.则∠D等于( )
如图,已知AB是⊙O的切线,点A为切点,连接OB交⊙O于点C,∠B=38°,点D是⊙O上一点,连接CD,AD.则∠D等于( )
 如图,已知AB是⊙O的切线,点A为切点,连接OB交⊙O于点C,∠B=38°,点D是⊙O上一点,连接CD,AD.则∠D等于( )
如图,已知AB是⊙O的切线,点A为切点,连接OB交⊙O于点C,∠B=38°,点D是⊙O上一点,连接CD,AD.则∠D等于( )| A. | 76° | B. | 38° | C. | 30° | D. | 26° |
17.若x<y成立,则下列不等式一定成立的是( )
| A. | 4x<3y | B. | -x<-y | C. | $\frac{x}{5}$>$\frac{y}{5}$ | D. | x-2015<y-2015 |
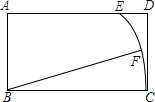 如图,在矩形ABCD中,AB=3,BC=5,以B为圆心BC为半径画弧交AD于点E,如果点F是弧EC的中点,联结FB,那么tan∠FBC的值为$\frac{1}{3}$.
如图,在矩形ABCD中,AB=3,BC=5,以B为圆心BC为半径画弧交AD于点E,如果点F是弧EC的中点,联结FB,那么tan∠FBC的值为$\frac{1}{3}$.