题目内容
2．
如图，在平行四边形ABCD中，AB=8，AD=4，E是AD的中点，在AB上取一点F，使AF=7．求证：△CBF∽△CDE．
分析 直接利用平行四边形的性质得出AE=DE=2，BF=1，AB=DC=8，AD=BC=4，再利用相似三角形的判定证明即可．
解答 证明：∵在平行四边形ABCD中，AB=8，AD=4，E是AD的中点，
∴AE=DE=2，BF=1，AB=DC=8，AD=BC=4，
∵$\frac{DE}{DC}=\frac{2}{8}=\frac{BF}{BC}=\frac{1}{4}$，∠D=∠B
∴△CBF∽△CDE．
点评 此题主要考查了平行四边形的性质以及相似三角形的判定，熟练应用相似三角形的判定是解题关键．
练习册系列答案
阅读快车系列答案
相关题目
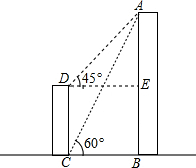如图，AB、CD为两栋建筑物，建筑物CD的高度为20m，从建筑物CD的顶部D点测得建筑物AB的顶部A点的仰角为45°，从建筑物CD的底部C点测得建筑物AB的顶部A点的仰角60°，求建筑物AB的高度（结果保留整数）（参考数据：$\sqrt{2}$≈1.41，$\sqrt{3}$≈1.73）
如图，已知点A、B、C在⊙O上，且AB=AC，∠BAC=40°，BD为⊙O的直径，则∠ADB=70°．
如图，正方形ABCD的边长为1cm，以CD为直径在正方形内画半圆，再以C为圆心，1cm长为半径画弧BD，则图中阴影部分的面积为$\frac{π}{8}$cm2．