题目内容
如图，四边形OABC为菱形，点B、C在以点O为圆心的 |
| EF |
|
| EF |
A、
| ||
B、
| ||
C、
| ||
D、
|
考点：弧长的计算,菱形的性质
专题：
分析：首先算出扇形OEF的圆心角，然后根据弧长的公式计算即可．
解答：
解：如图，连接OB．
由题意可知OA=OB=OC=OF=2cm，
∴△AOB，△BOC是等边三角形，
∴∠AOC=120°，
∵∠1=∠2，
∴∠EOF=120°，
故
的长为
=
π（cm）．
故选：C．
解：如图，连接OB．由题意可知OA=OB=OC=OF=2cm，
∴△AOB，△BOC是等边三角形，
∴∠AOC=120°，
∵∠1=∠2，
∴∠EOF=120°，
故
|
| EF |
| 120π×2 |
| 180 |
| 4 |
| 3 |
故选：C．
点评：此题主要考查了弧长的计算，解此题的关键是能利用菱形的性质求出扇形的半径和圆心角，从而求出弧长．
练习册系列答案
相关题目
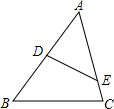如图：在△ABC中，点D、E分别在AB、AC上，∠ADE=∠C，且AD：AC=2：3，那么DE：BC等于（ ）| A、3：1 | B、1：3 |
| C、3：4 | D、2：3 |
如图，一个半径为6cm，面积为127πcm2的扇形纸片，现需要一个半径为R的圆形纸片，使两张纸片刚好合成圆锥体，则R=
如图，在Rt△ABC中，已知∠ACB=90°，AC=1，BC=3，将△ABC绕着点A按逆时针方向旋转30°，使得点B与点B′重合，点C与点C′重合，则图中阴影部分的面积为
如图，AB是⊙O的直径，弧BD=弧BC，∠A=25°．则∠BOD的度数为（ ）| A、12.5° | B、30° |
| C、40° | D、50° |
如图，△ABC是等边三角形，四边形ABDE与四边形ACFG都是长方形，且AE=AG．