题目内容
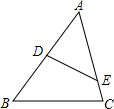如图：在△ABC中，点D、E分别在AB、AC上，∠ADE=∠C，且AD：AC=2：3，那么DE：BC等于（ ）| A、3：1 | B、1：3 |
| C、3：4 | D、2：3 |
考点：相似三角形的判定与性质
专题：
分析：根据由两对角相等的两个三角形相似可证明△ADE∽△ACB，利用相似三角形的性质：对应边的比值相等即可求出DE：BC的值．
解答：解：∵∠A=∠A，∠ADE=∠C，
∴△ADE∽△ACB，
∴DE：BC=AD：AC=2：3，
故选D．
∴△ADE∽△ACB，
∴DE：BC=AD：AC=2：3，
故选D．
点评：本题考查了相似三角形的判定和性质，题目比较简单，是中考常见题型．
练习册系列答案
相关题目
如图，AB是⊙O的直径，点C在⊙O上，连接BC，AC，作OD∥BC与过点A的切线交于点D，连接DC并延长交AB的延长线于点E．
反比例函数y=| k |
| x |
| A、①②③④ | B、①②③ |
| C、①②④ | D、②③④ |
下列车标图案中，是中心对称图形的是（ ）
A、 |
B、 |
C、 |
D、 |
如图，为了估算河的宽度，小明采用的办法是：在河的对岸选取一点A，在近岸取点D，B，使得A，D，B在一条直线上，且与河的边沿垂直，测得BD=10m，然后又在垂直AB的直线上取点C，并量得BC=30m．如果DE=20m，则河宽AD为（ ）| A、20m | ||
B、
| ||
| C、10m | ||
| D、30m |
若两个圆的半径分别为2和1，圆心距为3，则这两个圆的位置关系是（ ）
| A、内含 | B、内切 | C、相交 | D、外切 |
如图，热气球的探测器显示，从热气球点A处看我市一栋高楼顶部B点处的仰角为60°，看这栋高楼底部C点处的俯角为30°，热气球与高楼的水平距离为66m，求这栋高楼的高度．（结果精确到0.1m，参考数据：
如图，四边形OABC为菱形，点B、C在以点O为圆心的 |
| EF |
|
| EF |
A、
| ||
B、
| ||
C、
| ||
D、
|