题目内容
 如图,已知△OAB的顶点A(-3,0)、B(0,1)O(0,0).将△OAB绕点O按顺时针旋转90°得到△ODC,抛物线y=ax2+bx+c经过A、D、C三点.
如图,已知△OAB的顶点A(-3,0)、B(0,1)O(0,0).将△OAB绕点O按顺时针旋转90°得到△ODC,抛物线y=ax2+bx+c经过A、D、C三点.(1)求抛物线的解析式,并写出抛物线的顶点坐标;
(2)在给定的平面直角坐标中,画出(1)中抛物线;
(3)将(1)中的抛物线沿y轴平移m(m>0)个长度单位,使平移后抛物线的顶点落在直线y=-x上,试求出平移的方法和平移后的抛物线的解析式.
考点:二次函数综合题
专题:
分析:(1)根据旋转的性质得出D,C点坐标,进而利用待定系数法求二次函数解析式解析式,进而利用配方法求出抛物线顶点坐标;
(2)利用(1)中所求得出抛物线图象即可;
(3)利用平移的性质得出平移后解析式,进而得出其顶点坐标,再代入直线y=-x求出即可.
(2)利用(1)中所求得出抛物线图象即可;
(3)利用平移的性质得出平移后解析式,进而得出其顶点坐标,再代入直线y=-x求出即可.
解答: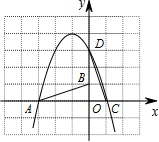 解:(1)∵A(-3,0)、B(0,1)、O(0,0),将△OAB绕点O按顺时针旋转90°得到△ODC,
解:(1)∵A(-3,0)、B(0,1)、O(0,0),将△OAB绕点O按顺时针旋转90°得到△ODC,
∴D(0,3)、C(1,0),
∴设抛物线的解析式为:y=a(x+3)(x-1),
将(0,3)代入得出:3=a(0+3)×(-1),
解得:a=-1,
∴y=-(x+3)(x-1)=-x2-2x+3=-(x+1)2+4,
∴抛物线的顶点坐标为:(-1,4);
(2)根据(1)中所求抛物线顶点坐标以及A,C,D点坐标,即可得出抛物线图象,如图所示:
(3)设抛物线平移后解析式为:y=-(x+1)2+4+m,
∴平移后顶点坐标为:(-1,4+m),代入y=-x得,m=-3,
∴将抛物线向下平移3个单位,
∴平移后解析式为:y=-(x+1)2+1.
 解:(1)∵A(-3,0)、B(0,1)、O(0,0),将△OAB绕点O按顺时针旋转90°得到△ODC,
解:(1)∵A(-3,0)、B(0,1)、O(0,0),将△OAB绕点O按顺时针旋转90°得到△ODC,∴D(0,3)、C(1,0),
∴设抛物线的解析式为:y=a(x+3)(x-1),
将(0,3)代入得出:3=a(0+3)×(-1),
解得:a=-1,
∴y=-(x+3)(x-1)=-x2-2x+3=-(x+1)2+4,
∴抛物线的顶点坐标为:(-1,4);
(2)根据(1)中所求抛物线顶点坐标以及A,C,D点坐标,即可得出抛物线图象,如图所示:
(3)设抛物线平移后解析式为:y=-(x+1)2+4+m,
∴平移后顶点坐标为:(-1,4+m),代入y=-x得,m=-3,
∴将抛物线向下平移3个单位,
∴平移后解析式为:y=-(x+1)2+1.
点评:此题主要考查了二次函数的平移以及图形的旋转以及配方法求二次函数顶点坐标等知识,正确记忆二次函数平移规律是解题关键.

练习册系列答案
相关题目
 如图所示,点D、E分别为线段CB、AC的中点,若ED=6,求线段AB的长度.
如图所示,点D、E分别为线段CB、AC的中点,若ED=6,求线段AB的长度. 如图,四边形ABCD是正方形,曲线DA1B1C1D1…叫做“正方形的渐开线”,其中弧
如图,四边形ABCD是正方形,曲线DA1B1C1D1…叫做“正方形的渐开线”,其中弧