题目内容
20.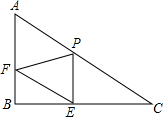 已知Rt△ABC中,∠B=90°,AC=20,AB=10,P是边AC上一点(不包括端点A、C),过点P作PE⊥BC于点E,过点E作EF∥AC,交AB于点F.设PC=x,
已知Rt△ABC中,∠B=90°,AC=20,AB=10,P是边AC上一点(不包括端点A、C),过点P作PE⊥BC于点E,过点E作EF∥AC,交AB于点F.设PC=x,PE=y.
(1)求y与x的函数关系式;
(2)是否存在点P使△PEF是Rt△?若存在,求此时的x的值;若不存在,请说明理由.
分析 (1)在Rt△ABC中,根据三角函数可求y与x的函数关系式;
(2)分三种情况:①如图1,当∠FPE=90°时,②如图2,当∠PFE=90°时,③当∠PEF=90°时,进行讨论可求x的值.
解答 解:(1)在Rt△ABC中,∠B=90°,AC=20,AB=10,
∴sinC=$\frac{1}{2}$,
∵PE⊥BC于点E,
∴sinC=$\frac{PE}{PC}$=$\frac{1}{2}$,
∵PC=x,PE=y, ∴y=$\frac{1}{2}$x(0<x<20);
∴y=$\frac{1}{2}$x(0<x<20);
(2)存在点P使△PEF是Rt△,
①如图1,当∠FPE=90°时,四边形PEBF是矩形,BF=PE=$\frac{1}{2}$x,
四边形APEF是平行四边形,PE=AF=$\frac{1}{2}$x,
∵BF+AF=AB=10,
∴x=10; ②如图2,当∠PFE=90°时,Rt△APF∽Rt△ABC,
②如图2,当∠PFE=90°时,Rt△APF∽Rt△ABC,
∠ARP=∠C=30°,AF=40-2x,
平行四边形AFEP中,AF=PE,即:40-2x=$\frac{1}{2}$x,
解得x=16;
③当∠PEF=90°时,此时不存在符合条件的Rt△PEF.
综上所述,当x=10或x=16,存在点P使△PEF是Rt△.
点评 考查了相似三角形的判定与性质,平行四边形的性质,矩形的性质,解直角三角形,注意分类思想的运用,综合性较强,难度中等.

练习册系列答案
相关题目
10.方程3x+y=9在正整数范围内的解的个数是( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 有无数个 |
5.调查作业:了解你所在小区家庭5月份用气量情况:
小天、小东和小芸三位同学住在同一小区,该小区共有300户家庭,每户家庭人数在2-5之间,这300户家庭的平均人数均为3.4.
小天、小东和小芸各自对该小区家庭5月份用气量情况进行了抽样调查,将收集的数据进行了整理,绘制的统计表分别为表1,表2和表3.
表1 抽样调查小区4户家庭5月份用气量统计表 (单位:m3)
表2 抽样调查小区15户家庭5月份用气量统计表 (单位:m3)
表3 抽样调查小区15户家庭5月份用气量统计表 (单位:m3)
根据以上材料回答问题:
小天、小东和小芸三人中,哪一位同学抽样调查的数据能较好地反映该小区家庭5月份用气量情况,并简要说明其他两位同学抽样调查的不足之处.
小天、小东和小芸三位同学住在同一小区,该小区共有300户家庭,每户家庭人数在2-5之间,这300户家庭的平均人数均为3.4.
小天、小东和小芸各自对该小区家庭5月份用气量情况进行了抽样调查,将收集的数据进行了整理,绘制的统计表分别为表1,表2和表3.
表1 抽样调查小区4户家庭5月份用气量统计表 (单位:m3)
| 家庭人数 | 2 | 3 | 4 | 5 |
| 用气量 | 14 | 19 | 21 | 26 |
| 家庭人数 | 2 | 2 | 2 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 4 |
| 用气量 | 10 | 11 | 15 | 13 | 14 | 15 | 15 | 17 | 17 | 18 | 18 | 18 | 18 | 20 | 22 |
| 家庭人数 | 2 | 2 | 2 | 3 | 3 | 3 | 3 | 3 | 3 | 4 | 4 | 4 | 4 | 5 | 5 |
| 用气量 | 10 | 12 | 13 | 14 | 17 | 17 | 18 | 19 | 20 | 20 | 22 | 26 | 31 | 28 | 31 |
小天、小东和小芸三人中,哪一位同学抽样调查的数据能较好地反映该小区家庭5月份用气量情况,并简要说明其他两位同学抽样调查的不足之处.
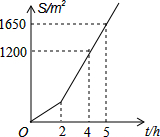 明君社区有一块空地需要绿化,某绿化组承担了此项任务,绿化组工作一段时间后,提高了工作效率.该绿化组完成的绿化面积S(单位:m2)与工作时间t(单位:h)之间的函数关系如图所示,则该绿化组提高工作效率前每小时完成的绿化面积是( )
明君社区有一块空地需要绿化,某绿化组承担了此项任务,绿化组工作一段时间后,提高了工作效率.该绿化组完成的绿化面积S(单位:m2)与工作时间t(单位:h)之间的函数关系如图所示,则该绿化组提高工作效率前每小时完成的绿化面积是( )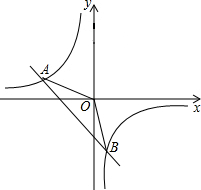 如图,在平面直角坐标系xOy中,一次函数y1=ax+b(a,b为常数,且a≠0)与反比例函数y2=$\frac{m}{x}$(m为常数,且m≠0)的图象交于A(-2,1),B(1,n).
如图,在平面直角坐标系xOy中,一次函数y1=ax+b(a,b为常数,且a≠0)与反比例函数y2=$\frac{m}{x}$(m为常数,且m≠0)的图象交于A(-2,1),B(1,n).