题目内容
 一个工人师傅要将一个正方形ABCD(四个角都是直角,四个边都相等)的余料,修剪成如四边形ABEF的零件.其中CE=
一个工人师傅要将一个正方形ABCD(四个角都是直角,四个边都相等)的余料,修剪成如四边形ABEF的零件.其中CE=| 1 |
| 4 |
考点:正方形的性质
专题:证明题
分析:根据两边对应成比例,夹角相等,两三角形相似求出△ADF和△FCE相似,根据相似三角形对应边成比例求出
=
=
,再求出
=
,从而得到
=
,然后判断出△ADF和△AFE相似,根据相似三角形对应角相等可得∠DAF=∠FAE,再根据角平分线的定义证明即可.
| CF |
| AD |
| EF |
| AF |
| 1 |
| 2 |
| DF |
| AD |
| 1 |
| 2 |
| DF |
| AD |
| EF |
| AF |
解答:证明:∵F是CD的中点,
∴DF=FC=
CD,
∵CE=
BC,
∴CE=
CD,
∴
=
=
,
又∵∠D=∠C=90°,
∴△ADF∽△FCE,
∴
=
=
,∠DAF=∠CFE,
∵∠ADF+∠DAF=90°,
∴∠ADF+∠CFE=90°,
∴∠AFE=90°,
∵
=
,
∴
=
,
又∵∠D=∠AFE=90°,
∴△ADF∽△AFE,
∴∠DAF=∠FAE,
∴AF平分∠DAE.
∴DF=FC=
| 1 |
| 2 |
∵CE=
| 1 |
| 4 |
∴CE=
| 1 |
| 2 |
∴
| CE |
| DF |
| CF |
| AD |
| 1 |
| 2 |
又∵∠D=∠C=90°,
∴△ADF∽△FCE,
∴
| CF |
| AD |
| EF |
| AF |
| 1 |
| 2 |
∵∠ADF+∠DAF=90°,
∴∠ADF+∠CFE=90°,
∴∠AFE=90°,
∵
| DF |
| AD |
| 1 |
| 2 |
∴
| DF |
| AD |
| EF |
| AF |
又∵∠D=∠AFE=90°,
∴△ADF∽△AFE,
∴∠DAF=∠FAE,
∴AF平分∠DAE.
点评:本题考查了正方形的性质,相似三角形的判定与性质,熟练掌握相似三角形的判定方法是解题的关键,难点在于求出△ADF和△AFE相似.

练习册系列答案
相关题目





 如图,BD是⊙O的切线,AB是⊙O的弦,且OA⊥OD.
如图,BD是⊙O的切线,AB是⊙O的弦,且OA⊥OD.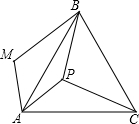 如图,P是正三角形ABC内的一点,且PA=6,PB=8,PC=10.若将△PAC绕点A逆时针旋转后,得到△MAB,则点P与点M之间的距离为
如图,P是正三角形ABC内的一点,且PA=6,PB=8,PC=10.若将△PAC绕点A逆时针旋转后,得到△MAB,则点P与点M之间的距离为