题目内容
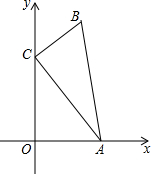 如图,在△ABC中,∠ACB=90°,AC=8,BC=3,点A、C分别在x轴、y轴上,当点A在x轴上运动时,点C随之在y轴上运动,在运动过程中,点B到原点O的最大距离为
如图,在△ABC中,∠ACB=90°,AC=8,BC=3,点A、C分别在x轴、y轴上,当点A在x轴上运动时,点C随之在y轴上运动,在运动过程中,点B到原点O的最大距离为考点:直角三角形斜边上的中线,线段的性质:两点之间线段最短,勾股定理
专题:
分析:点A,C分别在x轴、y轴上,当点A在x轴运动时,点C随之在y轴上运动,在运动过程中,点O在到AC的中点的距离不变.本题可通过设出AC的中点坐标,根据B、D、O在一条直线上时,点B到原点O的最大可得出答案.
解答: 解:作AC的中点D,连接OD、BD.
解:作AC的中点D,连接OD、BD.
∵OB≤OD+BD,
∴当O、D、B三点共线时OB取得最大值,
∵BD=
=
=5,OD=AD=
AC=4,
∴点B到原点O的最大距离为5+4=9.
故答案是:9.
 解:作AC的中点D,连接OD、BD.
解:作AC的中点D,连接OD、BD.∵OB≤OD+BD,
∴当O、D、B三点共线时OB取得最大值,
∵BD=
| BC2+CD2 |
| 32+42 |
| 1 |
| 2 |
∴点B到原点O的最大距离为5+4=9.
故答案是:9.
点评:此题主要考查了两点间的距离,以及勾股定理的应用,本题的难度较大,理解D到O的距离不变是解决本题的关键.

练习册系列答案
 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案
相关题目
2100的个位数字是( )
| A、2 | B、4 | C、6 | D、8 |

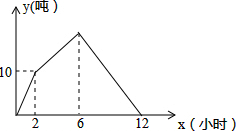 一个生产、装箱流水线,生产前没有积压产品,开始的2小时只生产,2小时后安排装箱(生产没有停止),6小时后生产停止只安排装箱,第12小时时生产流水线上刚好又没有积压产品,已知流水线的生产、装箱的速度保持不变,流水线上积压产品(没有装箱产品)y吨与流水线工作时间x(小时)之间的函数关系如图所示,则流水线上产品装箱的速度为
一个生产、装箱流水线,生产前没有积压产品,开始的2小时只生产,2小时后安排装箱(生产没有停止),6小时后生产停止只安排装箱,第12小时时生产流水线上刚好又没有积压产品,已知流水线的生产、装箱的速度保持不变,流水线上积压产品(没有装箱产品)y吨与流水线工作时间x(小时)之间的函数关系如图所示,则流水线上产品装箱的速度为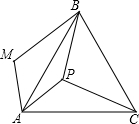 如图,P是正三角形ABC内的一点,且PA=6,PB=8,PC=10.若将△PAC绕点A逆时针旋转后,得到△MAB,则点P与点M之间的距离为
如图,P是正三角形ABC内的一点,且PA=6,PB=8,PC=10.若将△PAC绕点A逆时针旋转后,得到△MAB,则点P与点M之间的距离为