题目内容
19.已知关于x的一元二次方程x2+2(m+1)x+m2-1=0.(1)若方程有实数根,求实数m的取值范围;
(2)若方程两实数根分别为x1,x2,且满足x12+x22=16,求实数m的值.
分析 (1)根据方程有实根可得△≥0,进而可得[2(m+1)]2-4×1×(m2-1)≥0,再解即可;
(2)根据根与系数的关系可得x1+x2=-2(m+1),x1•x2=m2-1,再由完全平方公式可得x12+x22=(x1+x2)2-2x1x2,代入x1+x2=-2(m+1),x1•x2=m2-1可计算出m的值.
解答 解:(1)∵方程有实数根,
∴△≥0,
∴[2(m+1)]2-4×1×(m2-1)≥0,
解得:m≥-1;
(2)∵方程两实数根分别为x1,x2,
∴x1+x2=-2(m+1),x1•x2=m2-1,
∵x12+x22=16,
∴(x1+x2)2-2x1x2=16,
4(m+1)2-2(m2-1)=16,
解得:m=-5,m=1,
∵m≥-1,
∴m=1.
点评 此题主要考查了根与系数的关系,以及根的判别式,关键是掌握方程有实根则△≥0,x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=-$\frac{b}{a}$,
x1x2=$\frac{c}{a}$.

练习册系列答案
相关题目
4.已知下列结论:
①在数轴上只能表示无理数;
②任何一个无理数都能用数轴上的点表示;
③实数与数轴上的点一一对应;
④有理数有无限个,无理数有有限个.
⑤如果直角三角形的两边长分别是3,4,那么斜边长一定是5.
其中正确的结论是( )
①在数轴上只能表示无理数;
②任何一个无理数都能用数轴上的点表示;
③实数与数轴上的点一一对应;
④有理数有无限个,无理数有有限个.
⑤如果直角三角形的两边长分别是3,4,那么斜边长一定是5.
其中正确的结论是( )
| A. | ①②⑤ | B. | ②③ | C. | ③④ | D. | ②③④ |
11.在下列选项中,具有相反意义的量是( )
| A. | 盈利3万元与支出3万元 | |
| B. | 气温升高3℃与气温为-3℃ | |
| C. | 胜二局与负三局 | |
| D. | 甲乙两队篮球比赛比分分别为65:60与60:65 |
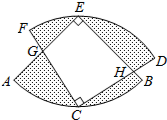 如图,两个半径相等的直角扇形的圆心分别在对方的圆弧上,半径AE、CF交于点G,半径BE、CD交于点H,且点C是弧AB的中点,若扇形的半径为$\sqrt{2}$,则图中阴影部分的面积等于π-2.
如图,两个半径相等的直角扇形的圆心分别在对方的圆弧上,半径AE、CF交于点G,半径BE、CD交于点H,且点C是弧AB的中点,若扇形的半径为$\sqrt{2}$,则图中阴影部分的面积等于π-2. 如图,已知在△ABC中,AD是BC边的中线,AE=EF=CF,BE与AD交于点G,求DF:GB的值.
如图,已知在△ABC中,AD是BC边的中线,AE=EF=CF,BE与AD交于点G,求DF:GB的值.