题目内容
18. 如图,在矩形ABCD中(AB<BC),BC=2,M为对角线BD的中点,连接CM,以CM为直径作圆O交BD于点E,连接AE,当直线AE与圆O相切时,AB的长为( )
如图,在矩形ABCD中(AB<BC),BC=2,M为对角线BD的中点,连接CM,以CM为直径作圆O交BD于点E,连接AE,当直线AE与圆O相切时,AB的长为( )| A. | $2-\sqrt{2}$ | B. | $3-\sqrt{6}$ | C. | $2\sqrt{2}-1$ | D. | $\sqrt{6}-\sqrt{2}$ |
分析 如图连接EC,作EN⊥AC于N,设OE=OM=OC=a,分别求出线段ME,EC,在RT△BEC中利用勾股定理求出a2,再在RT△ABC中求出线段AB即可.
解答 解:如图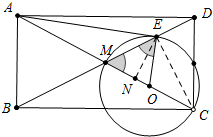 连接EC,作EN⊥AC于N,设OE=OM=OC=a,
连接EC,作EN⊥AC于N,设OE=OM=OC=a,
∵四边形ABCD是矩形,
∴AM=MC═BM=DM=2a,
∵AE是⊙O的切线,
∴∠AEO=90°,
∴AE=$\sqrt{A{O}^{2}-E{O}^{2}}$=$\sqrt{(3a)^{2}-{a}^{2}}$=2$\sqrt{2}$a,
∵$\frac{1}{2}$•AE•EO=$\frac{1}{2}$•AO•EN,
∴EN=$\frac{2\sqrt{2}}{3}$a,NO=$\sqrt{E{O}^{2}-E{N}^{2}}$=$\frac{1}{3}$a,
∴MN=$\frac{2}{3}$a,EM=$\sqrt{E{N}^{2}+M{N}^{2}}$=$\frac{2\sqrt{3}}{3}$a,EC=$\sqrt{E{N}^{2}+N{C}^{2}}$=$\frac{2\sqrt{6}}{3}$a,
在RT△BEC中,∵BE2+EC2=BC2,
∴(2a+$\frac{2\sqrt{3}}{3}$a)2+($\frac{2\sqrt{6}}{3}$a)2=22,
∴a2=$\frac{3}{6+2\sqrt{3}}$,
∴AB=$\sqrt{A{C}^{2}-B{C}^{2}}$=$\sqrt{\frac{48}{6+2\sqrt{3}}-4}$=$\sqrt{6}$-$\sqrt{2}$.
故选:D.
点评 本题考查切线的性质、矩形的性质、勾股定理等知识,解题的关键是设参数a,把相应的线段表示出来,利用勾股定理列出方程解决问题,题目比较难,计算半径复杂,掌握转化的思想,把问题转化为方程去思考.

 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案| A. | x=-1 | B. | x≠-1 | C. | x=0 | D. | x≠0 |
| A. | 摸到黑球、白球的可能性大小一样 | B. | 这个球一定是黑球 | ||
| C. | 事先能确定摸到什么颜色的球 | D. | 这个球可能是白球 |
| A. | 25 | B. | 5 | C. | -5 | D. | 0 |
 如图,在△ABC中,AD⊥BC,垂足为点D,若AC=6$\sqrt{2}$,∠C=45°,tan∠ABC=3,则BD等于( )
如图,在△ABC中,AD⊥BC,垂足为点D,若AC=6$\sqrt{2}$,∠C=45°,tan∠ABC=3,则BD等于( )| A. | 2 | B. | 3 | C. | 3$\sqrt{2}$ | D. | 2$\sqrt{3}$ |
①对顶角相等;
②两直线平行,内错角相等;
③两个锐角对应相等的两个直角三角形全等;
④有三个角是直角的四边形是矩形;
⑤平分弦的直径垂直于弦,并且平分弦所对的弧.
| A. | 1 个 | B. | 2 个 | C. | 3 个 | D. | 4 个 |
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
| A. | 调查市场上老酸奶的质量情况 | |
| B. | 调查某品牌圆珠笔芯的使用寿命 | |
| C. | 调查乘坐飞机的旅客是否携带了危禁物品 | |
| D. | 调查我市市民对2015年中考录取情况的知晓率 |
| A. | 任何有理数有倒数 | B. | -a一定是负数 | ||
| C. | 立方等于它本身的数有±1 | D. | 绝对值最小的数是0 |