Question

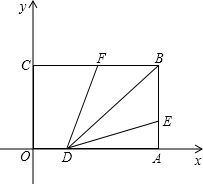如图，以矩形OABC的顶点O为原点，OA所在直线为x轴，OC所在直线为y轴，建立平面直角坐标系，已知OA=4厘米，OC=3厘米，线段OA上一动点D，以1厘米/s的速度从O点出发向终点A运动，线段AB上一动点E也以1厘米/s的速度从A点出发向终点B运动．当E点到达终点B后，D点继续运动直至到达终点A．
（1）试写出多边形ODEBC的面积S（平方厘米）与运动时间t（s）之间的函数关系式．
（2）在（1）的条件下，当多边形ODEBC的面积最小时，在坐标轴上是否存在点P，使△PDE为等腰三角形？若存在，求出点P的坐标；若不存在，请说明理由．
（3）在某一时刻将△BED沿着BD翻折，使点E恰好落在BC边的点F上．求出此时时间t的值．若此时在x轴上存在一点M，在y轴上存在一点N，使四边形MNFE的周长最小，试求出此时点M、N的坐标．

Answer 1

考点：四边形综合题

专题：压轴题

分析：（1）分为两种情况：当0≤t＜3时，求出OD=t，AD=4-t，AE=t，求出面积即可；当3≤t≤4时，E点运动至B点，求出面积即可；
（2）当0≤t＜3时，求出当t=2时，S_最小=10，当3≤t≤4时，求出当t=3时，S最小=

21

2

，得出当t=2时，S_最小=10
求出此时AD=2，AE=2，分为两种情况：①当P点在x轴上时，求出DE的长，分为PE=PD，DP=DE=2

2

，ED=EP=2

2

三种情况，求出即可；②当P点在y轴上时，分为PE=PD、DP=DE=2

2

、ED=EP=2

2

三种情况，关键等腰三角形性质求出即可；
（3）设AE=t，BE=3-t，BF=BE=3-t，AD=4-t，CF=4-BF=t+1．过D作DQ⊥BC于Q，则CQ=OD=t，QF=CF-CQ=1，得出方程（4-t）²+t²=10，求出t的值，求出E、F坐标，作点E关于x 轴的对称点E?为（4，-1），点F关于y轴的对称点F?为（-2，4），则直线E?F?与x轴、y轴的交点就是点M、点N，求出即可．

解答：解：（1）当0≤t＜3时，
∵OD=t，
∴AD=4-t，AE=t，
S五边形=4×3-

1

2

t(4-t)=

1

2

t2-2t+12；
当3≤t≤4时，E点运动至B点，S五边形=

1

2

×3(4+t)=

3

2

t+6；

（2）存在．
当0≤t＜3时，S=

1

2

t2-2t+12=

1

2

(t-2)2+10，即当t=2时，S_最小=10，
当3≤t≤4时，当t=3时，S最小=

21

2

，
综上所述，当t=2时，S_最小=10
此时AD=2，AE=2
①当P点在x轴上时，此时DE=

AD2+AE2

=2

2

；
当PE=PD时，点P与A点重合，即P（4，0）；
当DP=DE=2

2

时，P(2-2

2

，0)或P(2+2

2

，0)；
当ED=EP=2

2

时，有AD=AP=2，此时P（6，0）；

②当P点在y轴上时，
当PE=PD时，有AP是DE的中垂线，
则OA=OP=4，即P（0，4）；
当DP=DE=2

2

时，OP=

DP2-OD2

=2，即P（0，2）；
当ED=EP=2

2

时，由于EC=

BC2-BE2

=

15

＞2

2

，则这种情况不成立．
综上所述，满足条件的P点共有6个．

（3）设AE=t，则BE=3-t，BF=BE=3-t，AD=4-t，CF=4-BF=t+1．
过D作DQ⊥BC于Q，则CQ=OD=t，QF=CF-CQ=1，
∴DF²=DQ²+QF²=3²+1=10，
又∵DF=DE，
∴（4-t）²+t²=10，
解得t₁=1，t₂=3（不合题意，舍去），
此时，点E（4，1），点F（2，3），
则点E关于x 轴的对称点E?为（4，-1），点F关于y轴的对称点F?为（-2，3），
则直线E?F?与x轴、y轴的交点就是点M、点N，
设直线E?F?为y=kx+b，则

4k+b=-1 -2k+b=3

，解得，

k=- 2 3 b= 5 3

∴线E?F?为y=-

2

3

x+

5

3

．
∴M（

5

2

，0），（0，

5

3

）．

点评：本题考查了一次函数，二次函数，轴对称性质，二次函数的最值等知识点的应用，主要考查学生综合运用性质进行计算的能力，综合性比较强，难度偏大．