题目内容
当a>0时,关于x的一元二次方程ax2+2x+1=0无实数根,则抛物线y=ax2+2x+1的顶点在第 象限.
考点:抛物线与x轴的交点,二次函数的性质
专题:
分析:由根的判别式与根的关系求得a的取值范围a>1;然后根据不等式的性质知0<
<1;最后根据抛物线顶点坐标公式求得该抛物线的顶点(-
,1-
)位于第二象限.
| 1 |
| a |
| 1 |
| a |
| 1 |
| a |
解答:解:∵当a>0时,关于x的一元二次方程ax2+2x+1=0无实数根,
∴△=22-4a<0,
解得,a>1.
则0<
<1,
∴x=-
=-
<0,y=
=1-
>0
抛物线y=ax2+2x+1的顶点坐标位于(-
,1-
)第二象限.
故答案是:二.
∴△=22-4a<0,
解得,a>1.
则0<
| 1 |
| a |
∴x=-
| 2 |
| 2a |
| 1 |
| a |
| 4a-22 |
| 4a |
| 1 |
| a |
抛物线y=ax2+2x+1的顶点坐标位于(-
| 1 |
| a |
| 1 |
| a |
故答案是:二.
点评:本题考查了抛物线与x轴的交点、二次函数的性质.解答该题需要牢记抛物线的顶点坐标公式(-
,
).
| b |
| 2a |
| 4ac-b2 |
| 4a |

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
 如图,四边形OABC与CDEF均为菱形,且A(2,2)在反比例函数y=
如图,四边形OABC与CDEF均为菱形,且A(2,2)在反比例函数y=| k |
| x |
| A、S是变化的,因为菱形CDEF中只有C点的位置是确定的,其它三点都不是固定的 | ||||||||||
| B、当D点从C点到B点运动时,S逐渐增大 | ||||||||||
| C、从图上看,可以用两个菱形的面积减去两个三角形的面积,但E、F两点不确定,所以还是不能求出 | ||||||||||
D、如果连接CE,则CE∥OB,△OBE与△OBC同底(OB)共高,则S△OBE=S△OBC,OC=OA=2
|
在
,
,π和
四个实数中,其中的无理数是.( )
| 22 |
| 7 |
| 5 |
| 3 | 27 |
A、
| |||||
B、
| |||||
C、
| |||||
D、
|
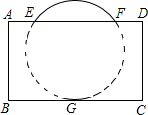 把球放在长方体纸盒内,球的一部分露出盒外,其截面如图所示.圆O与纸盒交于E、F、G三点,已知EF=CD=16cm.
把球放在长方体纸盒内,球的一部分露出盒外,其截面如图所示.圆O与纸盒交于E、F、G三点,已知EF=CD=16cm.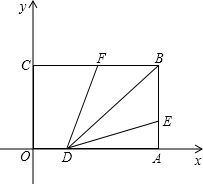 如图,以矩形OABC的顶点O为原点,OA所在直线为x轴,OC所在直线为y轴,建立平面直角坐标系,已知OA=4厘米,OC=3厘米,线段OA上一动点D,以1厘米/s的速度从O点出发向终点A运动,线段AB上一动点E也以1厘米/s的速度从A点出发向终点B运动.当E点到达终点B后,D点继续运动直至到达终点A.
如图,以矩形OABC的顶点O为原点,OA所在直线为x轴,OC所在直线为y轴,建立平面直角坐标系,已知OA=4厘米,OC=3厘米,线段OA上一动点D,以1厘米/s的速度从O点出发向终点A运动,线段AB上一动点E也以1厘米/s的速度从A点出发向终点B运动.当E点到达终点B后,D点继续运动直至到达终点A.