题目内容
若代数式a2+b2-4a+6b+10有最小值,那么这个最小值为 .
考点:配方法的应用,非负数的性质:偶次方
专题:计算题
分析:已知代数式配方后,利用非负数的性质即可求出最小值.
解答:解:原式=(a2-4a+4)+(b2+6b+9)-3=(a-2)2+(b+3)2-3,
则当a=2,b=-3时,最小值为-3.
故答案为:-3
则当a=2,b=-3时,最小值为-3.
故答案为:-3
点评:此题考查了配方法的应用,以及非负数的性质,熟练掌握完全平方公式是解本题的关键.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案
相关题目
为美化小区环境,某小区有一块面积为30平方米的等腰三角形草地,测得其一边长为10米.现要给这块三角形草地围上白色的低矮栅栏,现在准备这种低矮栅栏的长度分别有以下三种:①10+2
米;②20+2
米;③20+6
米,则符合要求的是( )
| 61 |
| 10 |
| 10 |
| A、只有①② | B、只有①③ |
| C、只有②③ | D、①②③ |
 如图,四边形OABC与CDEF均为菱形,且A(2,2)在反比例函数y=
如图,四边形OABC与CDEF均为菱形,且A(2,2)在反比例函数y=| k |
| x |
| A、S是变化的,因为菱形CDEF中只有C点的位置是确定的,其它三点都不是固定的 | ||||||||||
| B、当D点从C点到B点运动时,S逐渐增大 | ||||||||||
| C、从图上看,可以用两个菱形的面积减去两个三角形的面积,但E、F两点不确定,所以还是不能求出 | ||||||||||
D、如果连接CE,则CE∥OB,△OBE与△OBC同底(OB)共高,则S△OBE=S△OBC,OC=OA=2
|
下列调查方式合适的是( )
| A、为了了解九年级学生数学作业的时间,校长对九年级一班的3位同学进行了抽样调查 |
| B、为了了解全国青少年的睡眠时间,调研人员对某市七年级学生进行了调查 |
| C、为了了解重庆人民对建设“五个重庆”的感受,记者到某中学随机采访了20名老师 |
| D、为了了解我国新引进的一架飞机的安全性能,检查人员采用了普查的方式 |

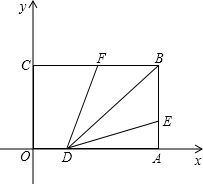 如图,以矩形OABC的顶点O为原点,OA所在直线为x轴,OC所在直线为y轴,建立平面直角坐标系,已知OA=4厘米,OC=3厘米,线段OA上一动点D,以1厘米/s的速度从O点出发向终点A运动,线段AB上一动点E也以1厘米/s的速度从A点出发向终点B运动.当E点到达终点B后,D点继续运动直至到达终点A.
如图,以矩形OABC的顶点O为原点,OA所在直线为x轴,OC所在直线为y轴,建立平面直角坐标系,已知OA=4厘米,OC=3厘米,线段OA上一动点D,以1厘米/s的速度从O点出发向终点A运动,线段AB上一动点E也以1厘米/s的速度从A点出发向终点B运动.当E点到达终点B后,D点继续运动直至到达终点A.