��Ŀ����
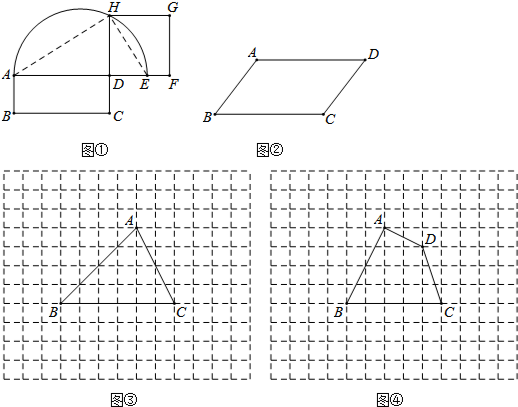
6���Ķ����еIJ��ϣ�ij��ѧѧϰС������������һ�����⣺��ͼ�����¶�Ϊ��ǣ���tan��=$\frac{1}{4}$��tan��=$\frac{3}{5}$�����+�µĶ�����
����ѧ����С������������������ģ���ͼ1���Ѧ����·��������������У�ʹ�á�ABD=������CBE=�£���BA��BCֱ��BD�����࣬����AC��
��1���۲�ͼ���֪����+��=��ABC=45�㣻
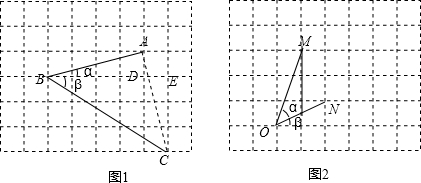
��2����ο�����ѧС��ķ���������⣺��������¶�Ϊ��ǣ���tan��=3��tan��=$\frac{1}{2}$ʱ����ͼ2�������������У���������������Ǧ���������MON=��-�£������MON�Ķ�����
���� ��1����BC2=AB2+AC2=2AB2���ó���ABC�ǵ���ֱ�������Σ��ҡ�BAC=90�㣬��ô��+��=��ABC=45�㣻
��2������MN����OM2=ON2+MN2=2ON2���ó���OMN�ǵ���ֱ�������Σ��ҡ�ONM=90�㣬��ô��-��=��MON=45�㣮
���  �⣺��1����ͼ1��
�⣺��1����ͼ1��
��BC2=32+52=34��AB2=42+12=17��AC2=42+12=17��
��BC2=AB2+AC2=2AB2��
���ABC�ǵ���ֱ�������Σ��ҡ�BAC=90�㣬
���+��=��ABC=45�㣮
�ʴ�Ϊ45��
��2����ͼ2������MN��
��OM2=32+12=10��ON2=22+12=5��MN2=22+12=5��
��OM2=ON2+MN2=2ON2��
���OMN�ǵ���ֱ�������Σ��ҡ�ONM=90�㣬
���-��=��MON=45�㣮
���� ���⿼���˽�ֱ�������Σ����ɶ��������涨��������ֱ�������ε��ж������ʣ���ͼ-Ӧ���������ͼ����������ṹ���м��㣬�ж���������ڵ��������ǵ���ֱ���������ǽ���Ĺؼ���

��ϰ��ϵ�д�
 �ǻ�С��ϰϵ�д�
�ǻ�С��ϰϵ�д�
�����Ŀ
15��Ϊ�˰������һ��������ͯ��ij����20��ͬѧ���������Ǿ����������±���
������20��ͬѧ�ľ������ǣ�������
| ���������λ��Ԫ�� | 20 | 50 | 80 | 100 |
| ������������� | 6 | 7 | 4 | 3 |
| A�� | 20Ԫ | B�� | 50Ԫ | C�� | 80Ԫ | D�� | 100Ԫ |
14����ͼ�٣��ڡ�ABC�У���ACB=90�㣬��CAB=30�㣬��ABD�ǵȱ������Σ���ͼ�ڣ����ı���ACBD�۵���ʹD��C�غϣ�EFΪ�ۺۣ����ACE������ֵΪ��������
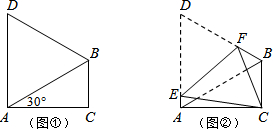

| A�� | $\frac{\sqrt{3}-1}{7}$ | B�� | $\frac{1}{7}$ | C�� | $\frac{\sqrt{3}}{12}$ | D�� | $\frac{\sqrt{3}-1}{6}$ |
1��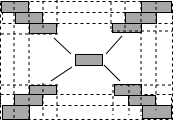 ��ͼ��ij�㳡����������1��1��С�����δ�ש��϶���̳ɳ����Σ�������������ɫС�����ι���82�飬���ɫС�����εĿ����ǣ�������
��ͼ��ij�㳡����������1��1��С�����δ�ש��϶���̳ɳ����Σ�������������ɫС�����ι���82�飬���ɫС�����εĿ����ǣ�������
 ��ͼ��ij�㳡����������1��1��С�����δ�ש��϶���̳ɳ����Σ�������������ɫС�����ι���82�飬���ɫС�����εĿ����ǣ�������
��ͼ��ij�㳡����������1��1��С�����δ�ש��϶���̳ɳ����Σ�������������ɫС�����ι���82�飬���ɫС�����εĿ����ǣ�������| A�� | 340 | B�� | 380 | C�� | 402 | D�� | 424 |
18��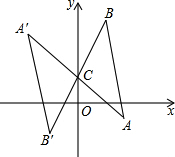 ��ͼ������ABC�Ƶ�C��0��1����ת180��õ���A��B��C�����A�������Ϊ��a��b�������A������Ϊ��������
��ͼ������ABC�Ƶ�C��0��1����ת180��õ���A��B��C�����A�������Ϊ��a��b�������A������Ϊ��������
 ��ͼ������ABC�Ƶ�C��0��1����ת180��õ���A��B��C�����A�������Ϊ��a��b�������A������Ϊ��������
��ͼ������ABC�Ƶ�C��0��1����ת180��õ���A��B��C�����A�������Ϊ��a��b�������A������Ϊ��������| A�� | ��-a��-b�� | B�� | ��-a��-b+2�� | C�� | ��-a��-b+1�� | D�� | ��-a��-b-1�� |
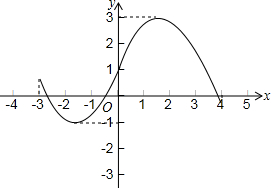 ��y�ǹ���x�ĺ�����H�dz�����H��0���������ڴ˺���ͼ���ϵ���һ���㣨x1��y1������x2��y2��������|y1-y2|��H����Ƹú���Ϊ�н纯���������������������г���H����Сֵ����Ϊ�ú����Ľ�ߣ�
��y�ǹ���x�ĺ�����H�dz�����H��0���������ڴ˺���ͼ���ϵ���һ���㣨x1��y1������x2��y2��������|y1-y2|��H����Ƹú���Ϊ�н纯���������������������г���H����Сֵ����Ϊ�ú����Ľ�ߣ�