题目内容
12. 在△ABC中,AB=AC,AB的垂直平分线交AB,AC于点D,E,△BCE的周长是8,AB-BC=2,则△ABC的周长是( )
在△ABC中,AB=AC,AB的垂直平分线交AB,AC于点D,E,△BCE的周长是8,AB-BC=2,则△ABC的周长是( )| A. | 13 | B. | 12 | C. | 11 | D. | 10 |
分析 根据线段垂直平分线的性质得出AE=CE,根据三角形周长求出BE+CE的值,求出AB,即可得出答案.
解答 解:∵DE是AB的垂直平分线,
∴AE=BE,
∵△BCE的周长为8,
∴AB+BC=8,
∵AB-BC=2,
∴AB=5,BC=3,
∵AB=AC,
∴AC=9,
∴△ABC的周长是:AC+AB+BC=,5+5+3=13.
故选A.
点评 本题考查了等腰三角形性质和线段垂直平分线性质,关键是求出AB和BC的长,熟练掌握线段垂直平分线的性质是解题的关键.

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
20.如果点A(x1,y1),B(x2,y2)都在反比例函数y=-$\frac{2}{x}$的图象上,并且x1<x2<0,那么下列各式正确的是( )
| A. | y2>y1>0 | B. | y1<y2<0 | C. | y1>y2>0 | D. | y2<y1<0 |
7.已知实数m,n满足m-n2=1,则代数式m2+2n2+4m-1的最小值等于( )
| A. | -12 | B. | -1 | C. | 4 | D. | 无法确定 |
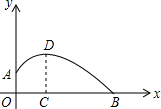 如图,一个运动员推铅球,铅球在点A处出手,出手时铅球离地面约1.6m,铅球落地点在点B处,铅球运行中在运动员前4m(即OC=4)达到最高点,最高点距离地面高度为3.2m,已知铅球经过的路线是抛物线,试在图示的直面坐标系中计算这个运动员的成绩.
如图,一个运动员推铅球,铅球在点A处出手,出手时铅球离地面约1.6m,铅球落地点在点B处,铅球运行中在运动员前4m(即OC=4)达到最高点,最高点距离地面高度为3.2m,已知铅球经过的路线是抛物线,试在图示的直面坐标系中计算这个运动员的成绩.