题目内容
 如图,在△ABC中,BP、CP分别是△ABC的外角∠DBC和∠ECB的平分线,
如图,在△ABC中,BP、CP分别是△ABC的外角∠DBC和∠ECB的平分线,(1)若∠ABC=20°,∠ACB=80°,则∠BPC=
(2)若∠A=70°,则∠BPC=
(3)试猜想∠BPC与∠A的数量关系,并证明你的猜想的正确性.
考点:三角形内角和定理,三角形的外角性质
专题:
分析:(1)先根据∠ABC=20°,∠ACB=80°得出∠DBC与∠BCE的度数,再根据BP、CP分别是△ABC的外角∠DBC和∠ECB的平分线得出∠PBC与∠PCB的度数,再根据三角形内角和定理即可得出∠BPC的度数;
(2)由角平分线的定义及三角形的一个外角等于与它不相邻的两个内角的和,得∠BCP=
∠BCE=
(∠A+∠CBA),∠CBP=
∠CBD=
(∠A+∠ACB);所以∠BCP+∠CBP=∠A+
(∠CBA+∠ACB),进而利用三角形的内角和定理求解;
(3)根据(1)、(2)的证明即可得出结论.
(2)由角平分线的定义及三角形的一个外角等于与它不相邻的两个内角的和,得∠BCP=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
(3)根据(1)、(2)的证明即可得出结论.
解答:解:(1)∵∠ABC=20°,∠ACB=80°,
∴∠DBC=180°-20°=160°,∠BCE=180°-80°=100°,
∵BP、CP分别是△ABC的外角∠DBC和∠ECB的平分线,
∴∠PBC=
∠DBC=80°,∠PCB=
∠BDE=50°,
∴∠BPC=180°-80°-50°=50°.
故答案为:50°;
(2)∵∠BCP=
∠BCE=
(∠A+∠CBA),∠CBP=
∠CBD=
(∠A+∠ACB),
∴∠BCP+∠CBP=∠A+
(∠CBA+∠ACB),
又∵∠BCP+∠CBP=180°-∠BPC,∠CBA+∠ACB=180°-∠A,
∴180°-∠BCP=∠A+
(180°-∠A),
∵∠A=70°,
∴∠BPC=55°.
故答案为:55°;
(3)猜想:∠A=180°-2∠BPC.
同(2)可得,180°-∠BCP=∠A+
(180°-∠A),
即∠A=180°-2∠BPC.
∴∠DBC=180°-20°=160°,∠BCE=180°-80°=100°,
∵BP、CP分别是△ABC的外角∠DBC和∠ECB的平分线,
∴∠PBC=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠BPC=180°-80°-50°=50°.
故答案为:50°;
(2)∵∠BCP=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴∠BCP+∠CBP=∠A+
| 1 |
| 2 |
又∵∠BCP+∠CBP=180°-∠BPC,∠CBA+∠ACB=180°-∠A,
∴180°-∠BCP=∠A+
| 1 |
| 2 |
∵∠A=70°,
∴∠BPC=55°.
故答案为:55°;
(3)猜想:∠A=180°-2∠BPC.
同(2)可得,180°-∠BCP=∠A+
| 1 |
| 2 |
即∠A=180°-2∠BPC.
点评:本题考查三角形外角的性质及三角形的内角和定理,解答的关键是沟通外角和内角的关系.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
关于-xy3z2,下列说法正确的是( )
| A、系数是0,次数是5 |
| B、系数是-1,次数是6 |
| C、系数是0,次数是6 |
| D、系数是1,次数是5 |
下列各式正确的是( )
| A、(23)2=25 |
| B、m7+m7=2m7 |
| C、x5•x=x5 |
| D、x4•x2=x8 |
 如图所示,△ABC的顶点是正方形网格的格点,则sinB的值为( )
如图所示,△ABC的顶点是正方形网格的格点,则sinB的值为( )A、
| ||||
B、
| ||||
C、
| ||||
| D、1 |
 如图,地面上直立着的两根高压电线杆相距50m(CD的长度),分别在高为30m的A处和20m的B处用钢索将两电线杆固定.
如图,地面上直立着的两根高压电线杆相距50m(CD的长度),分别在高为30m的A处和20m的B处用钢索将两电线杆固定.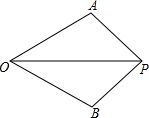 如图,已知∠AOP=∠BOP,OA=OB,求证:△OAP≌△OBP.
如图,已知∠AOP=∠BOP,OA=OB,求证:△OAP≌△OBP.