题目内容
19.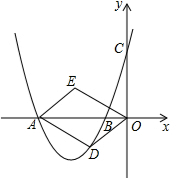 如图,抛物线y=$\frac{3}{4}$x2+$\frac{15}{4}$x+3与x轴交于A、B两点,点D为第三象限的抛物线上一动点.若四边形ODAE是以OA为对角线的平行四边形,且S?ODAE=6,请判断?ODAE是否为菱形?并说明理由.
如图,抛物线y=$\frac{3}{4}$x2+$\frac{15}{4}$x+3与x轴交于A、B两点,点D为第三象限的抛物线上一动点.若四边形ODAE是以OA为对角线的平行四边形,且S?ODAE=6,请判断?ODAE是否为菱形?并说明理由.
分析 结合菱形、平行四边形的性质来进行分析.如图,过点D作DH⊥x轴于点H,求出点D的坐标,进而判断平行四边形ODAE是否为菱形.
解答 解:如图,过点D作DH⊥x轴于点H.
∵S?ODAE=6,OA=4,
∴S△AOD=$\frac{1}{2}$OA•DH=3,
∴DH=$\frac{3}{2}$.
因为D在第三象限,所以D的纵坐标为负,且D在抛物线上,
∴$\frac{3}{4}$x2+$\frac{15}{4}$x+3=-$\frac{3}{2}$,
解得:x1=-2,x2=-3.
∴点D坐标为(-2,-$\frac{3}{2}$)或(-3,-$\frac{3}{2}$).
当点D为(-2,-$\frac{3}{2}$)时,DH垂直平分OA,平行四边形ODAE为菱形;
当点D为(-3,-$\frac{3}{2}$)时,OD≠AD,平行四边形ODAE不为菱形.
点评 本题综合考查了二次函数、平行四边形、菱形等知识点.涉及存在型问题,有一定的难度.在解题过程中,注意数形结合思想、分类讨论思想及方程思想等的应用.

练习册系列答案
相关题目
9.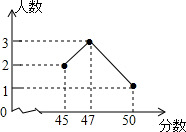 在2015年的体育中考中,某校6名学生的体育成绩统计如图,则这组数据的众数、中位数分别是( )
在2015年的体育中考中,某校6名学生的体育成绩统计如图,则这组数据的众数、中位数分别是( )
 在2015年的体育中考中,某校6名学生的体育成绩统计如图,则这组数据的众数、中位数分别是( )
在2015年的体育中考中,某校6名学生的体育成绩统计如图,则这组数据的众数、中位数分别是( )| A. | 3,2.5 | B. | 47,46 | C. | 47,47 | D. | 50,47 |
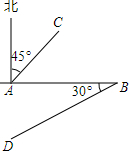 如图,是某油田的四口油井的位置图,图中1cm表示实际距离1.5km.请你仔细观察,并量一量图中的距离,用语言叙述这四口油井之间的位置关系.
如图,是某油田的四口油井的位置图,图中1cm表示实际距离1.5km.请你仔细观察,并量一量图中的距离,用语言叙述这四口油井之间的位置关系. 如图,已知在四边形ABED中,点C是线段AB的中点,且∠A=∠B=∠DCE,BE=2,AD=8,那么AC=4.
如图,已知在四边形ABED中,点C是线段AB的中点,且∠A=∠B=∠DCE,BE=2,AD=8,那么AC=4.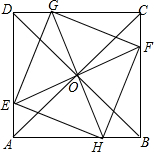 已知;如图,在正方形ABCD中,AC与BD相交于点O,EF,GH都过点O,分别交AD,BC于E,F,交CD,AB于G,H,EF⊥GH,求证:四边形EHFG是正方形.
已知;如图,在正方形ABCD中,AC与BD相交于点O,EF,GH都过点O,分别交AD,BC于E,F,交CD,AB于G,H,EF⊥GH,求证:四边形EHFG是正方形.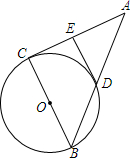 △ABC中,以BC为直径的圆O过边AB的中点D,DE⊥AC,求证:DE为⊙O的切线.
△ABC中,以BC为直径的圆O过边AB的中点D,DE⊥AC,求证:DE为⊙O的切线.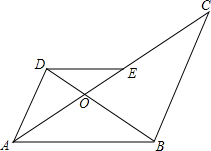 已知DE∥AB,OA2=OC•OE,求证:AD∥BC.
已知DE∥AB,OA2=OC•OE,求证:AD∥BC. 如图,在△ABC中,AB=AC,AD为BC边上的中线,E为AD上一点,则∠ABE与∠ACE的大小关系是怎样的?试说明理由.
如图,在△ABC中,AB=AC,AD为BC边上的中线,E为AD上一点,则∠ABE与∠ACE的大小关系是怎样的?试说明理由.