题目内容
14.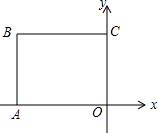 如图,O为坐标原点,矩形OABC中,A(-8,0),C(0,6),将矩形OABC绕点O旋转60°,得到矩形OA′B′C′,此时直线OA′与直线BC相交于P.则点P的坐标为(-2$\sqrt{3}$,6)或(2$\sqrt{3}$,6).
如图,O为坐标原点,矩形OABC中,A(-8,0),C(0,6),将矩形OABC绕点O旋转60°,得到矩形OA′B′C′,此时直线OA′与直线BC相交于P.则点P的坐标为(-2$\sqrt{3}$,6)或(2$\sqrt{3}$,6).
分析 作出图形,有两个解,利用直角三角形的30°的性质可以解决问题.
解答 解:如图,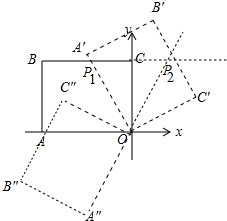 矩形OABC绕点O旋转60°,可能顺时针旋转,也可能逆时针旋转,所以有两种可能,见图.
矩形OABC绕点O旋转60°,可能顺时针旋转,也可能逆时针旋转,所以有两种可能,见图.
∵∠AOP1=60°,∠AOC=90°,
∴∠COP1=30°,
在RT△COP1中,∵OC=6,∠COP1=30°,
∴CP1=2$\sqrt{3}$,
∴点P1坐标为(-2$\sqrt{3}$,6),根据对称性,P1、P2关于y轴对称,
∴P2坐标(2$\sqrt{3}$,6).
故答案为(-2$\sqrt{3}$,6)或(2$\sqrt{3}$,6).
点评 本题考查矩形的性质.直角三角形的30度角的性质,解题的关键是正确画出图形,熟练掌握30度角的性质,善于观察利用对称性就很容易解决问题,善于中考常考题型.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
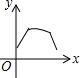
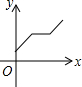
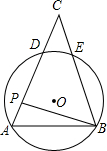 如图,⊙O经过△ABC的两个顶点A,B,与边AC,BC分别交于点D,E,点P从点A出发,沿A→D→E→C的路线匀速运动,设∠APB=y(单位:度),那么y与点P运动的时间x(单位:秒)的关系图大致是( )
如图,⊙O经过△ABC的两个顶点A,B,与边AC,BC分别交于点D,E,点P从点A出发,沿A→D→E→C的路线匀速运动,设∠APB=y(单位:度),那么y与点P运动的时间x(单位:秒)的关系图大致是( )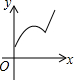
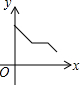
 如图,已知直线AB∥CD,BC∥DE,若∠B=60°,则∠D=120°.
如图,已知直线AB∥CD,BC∥DE,若∠B=60°,则∠D=120°.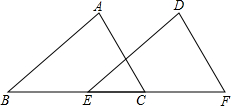 已知,如图,AC=DF,AC∥DF,BE=CF,请写出△ABC≌△DEF的理由.
已知,如图,AC=DF,AC∥DF,BE=CF,请写出△ABC≌△DEF的理由. 分别在直角坐标系中描出点(1)(0,0),(5,4),(3,0),(5,1)(5,-1),(3,0),(4,-2),(0,0);按描点的顺序连线.
分别在直角坐标系中描出点(1)(0,0),(5,4),(3,0),(5,1)(5,-1),(3,0),(4,-2),(0,0);按描点的顺序连线. 如图,在Rt△ABC中,∠ABC=90°,AB=8,BC=6,点D为AC边上的动点,点D从点C出发,沿边CA向点A运动,当运动到点A时停止,若设点D运动的时间为t秒.点D运动的速度为每秒1个单位长度.
如图,在Rt△ABC中,∠ABC=90°,AB=8,BC=6,点D为AC边上的动点,点D从点C出发,沿边CA向点A运动,当运动到点A时停止,若设点D运动的时间为t秒.点D运动的速度为每秒1个单位长度.