题目内容
17.在△ABC中,若AC2+BC2=AB2,∠A:∠B=1:2,则∠B的度数是60°.分析 由勾股定理的逆定理得出△ABC是直角三角形,∠C=90°,得出∠A+∠B=90°,再由已知条件即可得出∠B=60°.
解答 解:∵AC2+BC2=AB2,
∴△ABC是直角三角形,∠C=90°,
∴∠A+∠B=90°,
∵∠A:∠B=1:2,
∴∠A=30°,∠B=60°;
故答案为:60°.
点评 本题考查了勾股定理的逆定理、直角三角形的性质;熟练掌握勾股定理,证出△ABC是直角三角形是解决问题的关键.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
9.若两个非零有理数a,b,满足|a|=a,|b|=-b,a+b<0,则a,b的取值符合题意的是( )
| A. | a=2,b=-1 | B. | a=-2,b=1 | C. | a=1,b=-2 | D. | a=-1,b=-2 |
6. 如图,Rt△ABC中,∠ACB=90°,CD⊥AB于点D,则下列比值:$\frac{AC}{AB}$,$\frac{BC}{AB}$,$\frac{CD}{AC}$,$\frac{BD}{BC}$,其中可以表示cosB的有( )
如图,Rt△ABC中,∠ACB=90°,CD⊥AB于点D,则下列比值:$\frac{AC}{AB}$,$\frac{BC}{AB}$,$\frac{CD}{AC}$,$\frac{BD}{BC}$,其中可以表示cosB的有( )
 如图,Rt△ABC中,∠ACB=90°,CD⊥AB于点D,则下列比值:$\frac{AC}{AB}$,$\frac{BC}{AB}$,$\frac{CD}{AC}$,$\frac{BD}{BC}$,其中可以表示cosB的有( )
如图,Rt△ABC中,∠ACB=90°,CD⊥AB于点D,则下列比值:$\frac{AC}{AB}$,$\frac{BC}{AB}$,$\frac{CD}{AC}$,$\frac{BD}{BC}$,其中可以表示cosB的有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
7.下列说法错误的是( )
| A. | 48°21′36″的余角是41.64° | |
| B. | 点C是线段AB上的点,AB=10,AC=6,点D是线段BC的中点,则线段CD=2 | |
| C. | ∠AOC=60°,经过顶点O引一条射线OD,且∠AOD=25°,则∠COD=85° | |
| D. | 已知线段a,b如图 ,则尺规作图中 ,则尺规作图中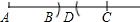 ,线段AD=2a-b ,线段AD=2a-b |
 射击比赛中,某队员的10次设计成绩如图所示,估计他的平均成绩是9环.
射击比赛中,某队员的10次设计成绩如图所示,估计他的平均成绩是9环.