题目内容
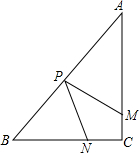 如图,在Rt△ABC中,∠C=90°,AC=4cm,BC=3com,动点M,N从点C同时出发,均以每秒1cm的速度分别沿CA、CB向终点A、B移动,同时动点P从点B出发,以每秒2cm的速度沿BA向终点A移动,连接PM、PN,设移动时间为t秒(0<t<2.5).
如图,在Rt△ABC中,∠C=90°,AC=4cm,BC=3com,动点M,N从点C同时出发,均以每秒1cm的速度分别沿CA、CB向终点A、B移动,同时动点P从点B出发,以每秒2cm的速度沿BA向终点A移动,连接PM、PN,设移动时间为t秒(0<t<2.5).(1)当t为何值时,以A、P、M为顶点三角形与△ABC相似?
(2)是否存在某一时刻t,使四边形APNC的面积为4.4cm2?
考点:相似三角形的判定与性质
专题:动点型
分析:(1)先根据勾股定理求出AB的长,以A、P、M为顶点三角形与△ABC相似分两种情况△AMP∽△ABC,△APM∽△ABC,再由相似三角形的对应边成比例即可得出t的值;
(2)过点P作PH⊥BC于点H,则∠PHB=90°,故可得出∠BPH∽△BAC,再由相似三角形的对应边成比例可得出PH=
t,由S四边形APNC=S△ABC-S△BPH即可得出结论.
(2)过点P作PH⊥BC于点H,则∠PHB=90°,故可得出∠BPH∽△BAC,再由相似三角形的对应边成比例可得出PH=
| 8 |
| 5 |
解答:解:∵在Rt△ABC中,∠C=90°,AC=4cm,BC=3cm,
∴AB2=AC2+BC2,即AB2=42+32,
∴AB=5.
(1)以A、P、M为顶点三角形与△ABC相似分两种情况.
①当△AMP∽△ABC时,
=
,即
=
,解得t=
;
②当△APM∽△ABC时,
=
,即
=
,解得t=0(舍去).
综上所述,当t=
秒时,以A、P、M为顶点三角形与△ABC相似;
(2)存在.
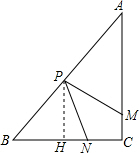 过点P作PH⊥BC于点H,则∠PHB=90°,
过点P作PH⊥BC于点H,则∠PHB=90°,
∵∠B=∠B,
∴∠BPH∽△BAC,
∴
=
,即
=
,解得PH=
t.
∵四边形APNC的面积为4.4cm2,
∴
×4×3-
×(3-t)•
t=4.4,
解得t1=1,t2=2.
答:1秒或2秒时,四边形APNC的面积为4.4cm2.
∴AB2=AC2+BC2,即AB2=42+32,
∴AB=5.
(1)以A、P、M为顶点三角形与△ABC相似分两种情况.
①当△AMP∽△ABC时,
| AP |
| AC |
| AM |
| AB |
| 5-2t |
| 4 |
| 4-t |
| 5 |
| 3 |
| 2 |
②当△APM∽△ABC时,
| AM |
| AC |
| AP |
| AB |
| 4-t |
| 4 |
| 5-2t |
| 5 |
综上所述,当t=
| 3 |
| 2 |
(2)存在.
 过点P作PH⊥BC于点H,则∠PHB=90°,
过点P作PH⊥BC于点H,则∠PHB=90°,∵∠B=∠B,
∴∠BPH∽△BAC,
∴
| BP |
| BA |
| PH |
| AC |
| 2t |
| 5 |
| PH |
| 4 |
| 8 |
| 5 |
∵四边形APNC的面积为4.4cm2,
∴
| 1 |
| 2 |
| 1 |
| 2 |
| 8 |
| 5 |
解得t1=1,t2=2.
答:1秒或2秒时,四边形APNC的面积为4.4cm2.
点评:本题考查的是相似三角形的判定与性质,熟知相似三角形的对应边成比例是解答此题的关键.

练习册系列答案
相关题目
四个角都相等,且邻边相等的四边形是( )
| A、平行四边形 | B、菱形 |
| C、矩形 | D、正方形 |
 如图:已知平行四边形ABCD中,K是BC上一点,且
如图:已知平行四边形ABCD中,K是BC上一点,且| BK |
| KC |
| 3 |
| 4 |
| BE |
| ED |
A、
| ||
B、
| ||
C、
| ||
D、
|
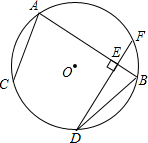 如图,已知AB、AC是⊙O的弦,D为弧BC的中点,弦DF⊥AB于E,AC=2,AB=3,则BE的长为( )
如图,已知AB、AC是⊙O的弦,D为弧BC的中点,弦DF⊥AB于E,AC=2,AB=3,则BE的长为( )| A、1 | ||
B、
| ||
C、
| ||
D、
|
给出下列说法:①0是整数;②-3.2是负分数;③5.6不是正数;④自然数一定是正数;⑤负分数一定是负有理数.其中正确的有( )
| A、1个 | B、2个 | C、3个 | D、4个 |
 在△ABC中,BD为AC边的垂线,CD=2,AD=4,tan∠ABC=
在△ABC中,BD为AC边的垂线,CD=2,AD=4,tan∠ABC= 如图,Rt△ABC中∠C=90°,AD•AC=AE•AB,求证:DE⊥AB.
如图,Rt△ABC中∠C=90°,AD•AC=AE•AB,求证:DE⊥AB. 如图,能与∠1构成同位角的角有
如图,能与∠1构成同位角的角有