题目内容
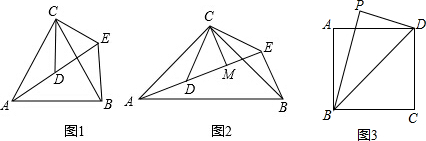
5．
如图，①如果∠1=∠2，那么根据内错角相等，两直线平行可得AB∥CD；
②如果∠DAB+∠ABC=180°，那么根据同旁内角互补，两直线平行，可得AB∥BC；
③当AB∥CD 时，根据两直线平行，同旁内角互补，得∠C+∠ABC=180°；
④当AE∥BC时，根据两直线平行，内错角相等，得∠C=∠3．
分析 根据平行线的判定定理得到①②的结论，根据平行线的性质定理得到③④的结论．
解答 解：①如果∠1=∠2，那么根据内错角相等，两直线平行可得AB∥CD；
②如果∠DAB+∠ABC=180°，那么根据同旁内角互补，两直线平行，可得AB∥BC；
③当AB∥CD 时，根据两直线平行，同旁内角互补，得∠C+∠ABC=180°；
④当AE∥BC时，根据两直线平行，内错角相等，得∠C=∠3．
点评 本题考查了平行线的判定和性质，熟练掌握平行线的判定定理和性质定理是解题的关键．
练习册系列答案
相关题目
15．已知在平面直角坐标系中，点M到x轴的距离为1，到y轴的距离为2，并且点M在第三象限，则点M的坐标为（ ）
| A． | （2，-1） | B． | （-2，-1） | C． | （-1，2） | D． | （1，-2） |
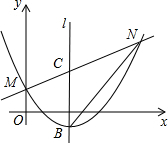如图，直线y=$\frac{1}{2}$x+1与抛物线y=$\frac{1}{2}$x2-bx+l交于不同的两点M、N（点M在点N的左侧）．
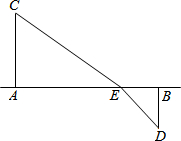如图所示铁路上A、B两站（视为两个点）相距25km，C、D为两村庄（视为两个点），CA⊥AB于点A，DB⊥AB于点B，已知CA=15km，DB=10km．现要在A．B之间建一个土特产收购站E，当AE=xkm时
10．下列命题的逆命题不正确的是（ ）
| A． | 菱形的四条边都相等 | B． | 两直线平行，内错角相等 | ||
| C． | 等腰三角形的两个底角相等 | D． | 全等三角形的对应角相等 |
