题目内容
8.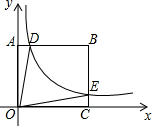 如图,双曲线y=$\frac{k}{x}$(k>0)经过矩形OABC的边BC上的点E,且2CE=BE,交AB于点D.若四边形ODBE的面积为8,则k=8.
如图,双曲线y=$\frac{k}{x}$(k>0)经过矩形OABC的边BC上的点E,且2CE=BE,交AB于点D.若四边形ODBE的面积为8,则k=8.
分析 根据题意可得S△OCE=S△OBE=S△OBD=S△DOA=$\frac{1}{4}$S矩形OABC,由四边形ODBE的面积为8,可得矩形ABCO的面积为16,进而可以算出k的值.
解答  连接BO,由(1)可知D、E是AB、BC的中点,
连接BO,由(1)可知D、E是AB、BC的中点,
S△OCE=S△OBE=S△OBD=S△DOA=$\frac{1}{4}$S矩形OABC,
∵四边形ODBE的面积为8,
∴S矩形OCBA=16,
∴ab=16,
即k=$\frac{1}{2}$ab=$\frac{1}{2}$×16=8.
故答案是:8.
点评 主要考查了反比例函数y=$\frac{k}{x}$中k的几何意义,即过双曲线上任意一点引x轴、y轴垂线,所得三角形面积为$\frac{1}{2}$|k|,是经常考查的一个知识点;这里体现了数形结合的思想,做此类题一定要正确理解k的几何意义.

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目
3.当x=( )时,分式$\frac{x+3}{|x|-2}$无意义( )
| A. | x=-3 | B. | x=2 | C. | x=-2 | D. | x=±2 |
13.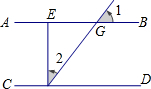 如图,若AB∥CD,EF⊥CD,∠1=54°,则∠2为( )
如图,若AB∥CD,EF⊥CD,∠1=54°,则∠2为( )
 如图,若AB∥CD,EF⊥CD,∠1=54°,则∠2为( )
如图,若AB∥CD,EF⊥CD,∠1=54°,则∠2为( )| A. | 54° | B. | 46° | C. | 44° | D. | 36° |
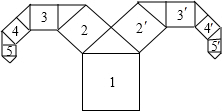 今年是农历羊年.如图所示是一种“羊头”形图案,其作法是,从正方形1开始,以它的一边为斜边,向外作等腰直角三角形,然后再以其直角边为边,分别向外作正方形2、3、4、…,和2′、3′、4′、…,依此类推.若正方形10的边长为1cm,则正方形1的边长16$\sqrt{2}$cm.
今年是农历羊年.如图所示是一种“羊头”形图案,其作法是,从正方形1开始,以它的一边为斜边,向外作等腰直角三角形,然后再以其直角边为边,分别向外作正方形2、3、4、…,和2′、3′、4′、…,依此类推.若正方形10的边长为1cm,则正方形1的边长16$\sqrt{2}$cm.