题目内容
17.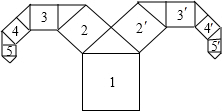 今年是农历羊年.如图所示是一种“羊头”形图案,其作法是,从正方形1开始,以它的一边为斜边,向外作等腰直角三角形,然后再以其直角边为边,分别向外作正方形2、3、4、…,和2′、3′、4′、…,依此类推.若正方形10的边长为1cm,则正方形1的边长16$\sqrt{2}$cm.
今年是农历羊年.如图所示是一种“羊头”形图案,其作法是,从正方形1开始,以它的一边为斜边,向外作等腰直角三角形,然后再以其直角边为边,分别向外作正方形2、3、4、…,和2′、3′、4′、…,依此类推.若正方形10的边长为1cm,则正方形1的边长16$\sqrt{2}$cm.
分析 根据等腰直角三角形直角边等于斜边的$\frac{\sqrt{2}}{2}$倍,求出第n个正方形的边长与第1个正方形的边长的关系式,然后把正方形10的边长1cm代入进行计算即可得解.
解答 解:根据题意,设正方形1的边长为a,则正方形②的边长为$\frac{\sqrt{2}}{2}$a,
正方形③的边长为:($\frac{\sqrt{2}}{2}$)2a,
正方形④的边长为:($\frac{\sqrt{2}}{2}$3a,
…,
依此类推,正方形n的边长为:($\frac{\sqrt{2}}{2}$)n-1a,
∵正方形10的边长为1cm,
∴正方形1的边长=16$\sqrt{2}$cm.
故答案为:16$\sqrt{2}$cm.
点评 本题考查了正方形的性质,等腰直角三角形的性质直角边等于斜边的$\frac{\sqrt{2}}{2}$倍的性质,求出第n个正方形的边长与第1个正方形的边长的关系式是解题的关键.

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目
2.若关于x的不等式mx-n>0的解集是$x<\frac{1}{7}$,则关于x的不等式(m+n)x>n-m的解集是( )
| A. | x<-$\frac{3}{4}$ | B. | x>-$\frac{3}{4}$ | C. | x>$\frac{3}{4}$ | D. | x<$\frac{3}{4}$ |
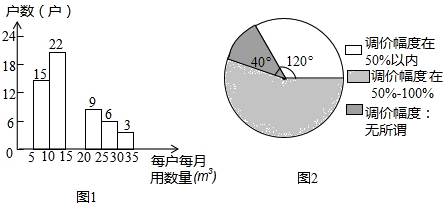
7.A市为制定居民用水价格调整方案,就每月的用水量、可承受的水价调整幅度等进行民意调查,调查采用随机抽样的方式.图1、图2为某一小区的调查数据统计图.
已知被调查居民每户每月的用水量在5m3~35m3之间,被调查的居民中对居民用水价格调价幅度抱“无所谓”态度的有8户,试回答下列问题:
(1)请补全图1的统计图;
(2)被调查居民用水量的中位数落在什么范围内:10m3~15m3(直接填写范围即可,如5m3~35m3等);
(3)若采用阶梯式累进制调价方案(如下表所示),试估计该小区有百分之几的居民用水费用的增长幅度不超过50%?
阶梯式累进制自来水调价方案
已知被调查居民每户每月的用水量在5m3~35m3之间,被调查的居民中对居民用水价格调价幅度抱“无所谓”态度的有8户,试回答下列问题:
(1)请补全图1的统计图;
(2)被调查居民用水量的中位数落在什么范围内:10m3~15m3(直接填写范围即可,如5m3~35m3等);
(3)若采用阶梯式累进制调价方案(如下表所示),试估计该小区有百分之几的居民用水费用的增长幅度不超过50%?
阶梯式累进制自来水调价方案
| 级数 | 用水量范围 | 现行价格(元/m3) | 调整后价格(元/m3) |
| 第一级 | 0~15m3(含15m3) | 1.80 | 2.50 |
| 第二级 | 15m3以上 | 1.80 | 3.30 |

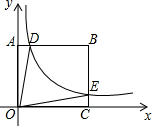 如图,双曲线y=$\frac{k}{x}$(k>0)经过矩形OABC的边BC上的点E,且2CE=BE,交AB于点D.若四边形ODBE的面积为8,则k=8.
如图,双曲线y=$\frac{k}{x}$(k>0)经过矩形OABC的边BC上的点E,且2CE=BE,交AB于点D.若四边形ODBE的面积为8,则k=8. 如图,小红用一张长方形纸片ABCD进行折纸,已知AB=8cm,BC=10cm.当小红折叠时,顶点D落在BC边上的点F处(折痕为AE),求EC.
如图,小红用一张长方形纸片ABCD进行折纸,已知AB=8cm,BC=10cm.当小红折叠时,顶点D落在BC边上的点F处(折痕为AE),求EC.