计算:(1)$\frac{x-y}{x+y}$÷(x-y)$\frac{1}{x-y}$,(2)$\frac{3}{x-4}$-$\frac{24}{{x}^{2}-16}$．题目和参考答案——青夏教育精英家教网—

题目内容

11．计算：
（1）$\frac{x-y}{x+y}$÷（x-y）$\frac{1}{x-y}$；
（2）$\frac{3}{x-4}$-$\frac{24}{{x}^{2}-16}$．

分析（1）先将除法统一为乘法，然后利用约分即可求出答案．
（2）先将分母因式分解，然后进行对分式进行通分和化简即可求出答案

解答解：（1）原式=$\frac{x-y}{x+y}$×$\frac{1}{x-y}$×$\frac{1}{x-y}$=$\frac{1}{{x}^{2}-{y}^{2}}$
（2）原式=$\frac{3（x+4）}{（x-4）（x+4）}$-$\frac{24}{（x+4）（x-4）}$=$\frac{3}{x+4}$

点评本题考查分式的混合运算，解题关键是熟练运用因式分解，以及分式的基本性质，本题属于基础题型．

练习册系列答案

相关题目

1．

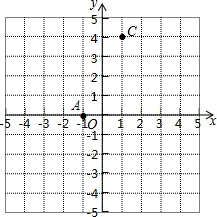如图，A（-1，0），C（1，4），点B在x轴上，且AB=4．
（1）求点B的坐标；
（2）求△ABC的面积；
（3）在y轴上是否存在点P，使以A、B、P三点为顶点的三角形的面积为7？若存在，请直接写出点P的坐标；若不存在，请说明理由．

2．

如图，已知A（2，3），B（1，1），C（4，1），M（6，3）．
（1）将△ABC平原得到△A₁B₁C₁，其中点A，B，C的对应点分别是A₁，B₁，C₁，且点A₁的坐标是（3，6），在图中画出△A₁B₁C₁．
（2）将（1）中的△A₁B₁C₁绕点M顺时针旋转90°，画出旋转后的△A₂B₂C₂（其中点A₂，B₂，C₂的对应点分别是A₁，B₁，C₁），并写出点A₂，B₂，C₂的坐标．
（3）（2）中的△A₂B₂C₂能通过旋转△ABC得到吗？若能，请写出旋转的方案．

x₁=7，x₂=-7

x₁=-$\sqrt{7}$，x₂=$\sqrt{7}$

6．

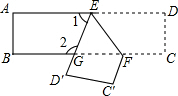如图，将一张长方形的纸片沿EF折叠后，点D、C分别落在点D′、C′的位置上，ED′与BC的交点为点G，若∠EFG=50°，求∠EGB的度数．

16．

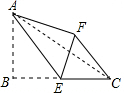如图，在△ABC中，∠B=90°，AB=4，BC=6，点E为BC的中点，将△ABE沿AE折叠，使点B落在点F处，连CF，求CF的长．

3．

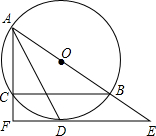如图，⊙O是△ABC的外接圆，AB为直径，∠BAC的平分线交⊙O于点D，过点D的切线分别交AB，AC的延长线于点E，F
（1）求证：AF⊥EF；
（2）若AF=3.5，AB=5，求CF的长度．

20．

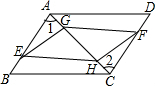如图，已知平行四边形ABCD中，BE=DF，AG=CH，求证：GEHF是平行四边形．

18．

如图，教室里放有一台饮水机，课间同学们依次用茶杯接水，假设接水过程中水不发生泼洒，每个同学所接的水量相等；两个放水管同时打开时，它们的流量相同．若只打开一个阀门2分钟后，再同时打开第二个阀门，（放水过程中阀门不关）．饮水机的存水量（升）与放水时间（分）之间的关系如表所示：

放水时间（分）	0	2	12	…
饮水机中存水量（升）	18	17	8	…

（1）根据表格信息可得：只开一个阀门每分钟出水量为0.5升，两个阀门同时打开每分钟总出水量为0.9升；
（2）如果从开始到2分钟时恰好有4个同学接水结束，则课间共有22个同学依次接水需要几分钟？
（3）按题中所给的放水方法，课间10分钟内最多有多少个同学能及时接完水？

试题分类