题目内容
3.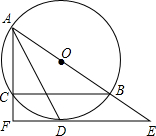 如图,⊙O是△ABC的外接圆,AB为直径,∠BAC的平分线交⊙O于点D,过点D的切线分别交AB,AC的延长线于点E,F
如图,⊙O是△ABC的外接圆,AB为直径,∠BAC的平分线交⊙O于点D,过点D的切线分别交AB,AC的延长线于点E,F(1)求证:AF⊥EF;
(2)若AF=3.5,AB=5,求CF的长度.
分析 (1)连接OD,如图,利用角平分线定义得到∠1=∠2,加上∠2=∠3,则∠1=∠3,所以OD∥AF,再利用切线的性质得OD⊥EF,于是利用平行线的性质可得到AF⊥EF;
(2)连接OC,OD交BC于H,如图,设CF=x,先判断四边形CFDH为矩形得到HD=CF=x,再证明OH为△ACB的中位线得到OH=$\frac{1}{2}$($\frac{7}{2}$-x),则利用OH=OD-DH=$\frac{5}{2}$-x得到$\frac{1}{2}$($\frac{7}{2}$-x)=$\frac{5}{2}$-x,然后解方程求出x即可.
解答 (1)证明:连接OD,如图,
∵∠BAC的平分线交⊙O于点D,
∴∠1=∠2,
∵OA=OD,
∴∠2=∠3,
∴∠1=∠3,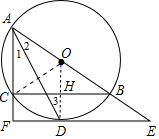
∴OD∥AF,
∵EF为切线,
∴OD⊥EF,
∴AF⊥EF;
(2)解:连接OC,OD交BC于H,如图,设CF=x,
∵AB为直径,
∴∠ACB=90°,
而AF⊥EF,OD⊥EF,
∴四边形CFDH为矩形,
∴HD=CF=x,
∵OH∥AC,OA=OB,
∴OH为△ACB的中位线,
∴OH=$\frac{1}{2}$AC=$\frac{1}{2}$(AF-CF)=$\frac{1}{2}$($\frac{7}{2}$-x)
而OH=OD-DH=$\frac{5}{2}$-x,
∴$\frac{1}{2}$($\frac{7}{2}$-x)=$\frac{5}{2}$-x,解得x=$\frac{3}{2}$,
即CF的长为$\frac{3}{2}$.
点评 本题考查了切线的性质:圆的切线垂直于经过切点的半径.若出现圆的切线,必连过切点的半径,构造定理图,得出垂直关系.也考查了圆周角定理.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
 用小正方体搭一个几何体,使得从上面和正面看它的图形如图所示.
用小正方体搭一个几何体,使得从上面和正面看它的图形如图所示. 如图所示,AM平分∠BAC,AM∥EN,试证明∠E=∠CDN.
如图所示,AM平分∠BAC,AM∥EN,试证明∠E=∠CDN.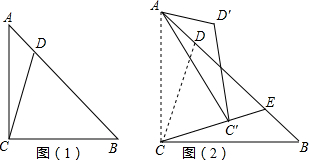
 青藏铁路于2006年7月1日胜利通车,青藏高原天堑变通途,圆了几代人的梦想.作为世界上海拔最高,施工难度最大的铁路,青藏铁路全县有一座大桥-拉萨河大桥(如图)全长920多米,其中主桥长800米,小明在去年暑假乘T22次列车从北京到拉萨游玩,小明为了探究T22次列车的长度与速度,记录了以下两个数据:
青藏铁路于2006年7月1日胜利通车,青藏高原天堑变通途,圆了几代人的梦想.作为世界上海拔最高,施工难度最大的铁路,青藏铁路全县有一座大桥-拉萨河大桥(如图)全长920多米,其中主桥长800米,小明在去年暑假乘T22次列车从北京到拉萨游玩,小明为了探究T22次列车的长度与速度,记录了以下两个数据: 如图是某住宅的平面结构示意图,图中标注了有关尺寸(墙体厚度勿略不计,单位:m).
如图是某住宅的平面结构示意图,图中标注了有关尺寸(墙体厚度勿略不计,单位:m).