题目内容
20.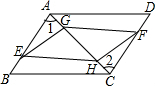 如图,已知平行四边形ABCD中,BE=DF,AG=CH,求证:GEHF是平行四边形.
如图,已知平行四边形ABCD中,BE=DF,AG=CH,求证:GEHF是平行四边形.
分析 根据SAS可以证明△AEG≌△CFH.从而得到GE=HF,∠AGE=∠CHF.根据等角的补角相等,可以证明∠EGH=∠FHG,则GE∥HF.根据一组对边平行且相等的四边形是平行四边形即可得出结论.
解答 证明:在平行四边形ABCD中,AB∥CD,
∴∠EAG=∠FCH.AB=CD,
∵BE=DF,
∴AE=CF,
在△AEG和△CFH中,$\left\{\begin{array}{l}{AG=CH}&{\;}\\{∠EAG=∠FCH}&{\;}\\{AE=CF}&{\;}\end{array}\right.$,
∴△AEG≌△CFH(SAS).
∴GE=HF,∠AGE=∠CHF,
∴∠EGH=∠FHG,
∴GE∥HF.
∴四边形GEHF是平行四边形.
点评 此题考查了平行四边形的性质和判定、全等三角形的判定与性质.熟练掌握平行四边形的性质,证明三角形全等是解决问题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案
相关题目
10.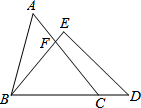 如图,在△ABC和△BDE中,点C在边BD上,边AC交边BE于点F.若AC=BD,AB=ED,BC=BE,则∠ACB等于( )
如图,在△ABC和△BDE中,点C在边BD上,边AC交边BE于点F.若AC=BD,AB=ED,BC=BE,则∠ACB等于( )
 如图,在△ABC和△BDE中,点C在边BD上,边AC交边BE于点F.若AC=BD,AB=ED,BC=BE,则∠ACB等于( )
如图,在△ABC和△BDE中,点C在边BD上,边AC交边BE于点F.若AC=BD,AB=ED,BC=BE,则∠ACB等于( )| A. | ∠EDB | B. | ∠BED | C. | 2∠ABF | D. | $\frac{1}{2}$∠AFB |
7.生活中的“八宝粥”易拉罐同学们都很熟悉,你认为“八宝粥”易拉罐类似于( )
| A. | 棱柱 | B. | 圆柱 | C. | 圆锥 | D. | 长方体 |
 青藏铁路于2006年7月1日胜利通车,青藏高原天堑变通途,圆了几代人的梦想.作为世界上海拔最高,施工难度最大的铁路,青藏铁路全县有一座大桥-拉萨河大桥(如图)全长920多米,其中主桥长800米,小明在去年暑假乘T22次列车从北京到拉萨游玩,小明为了探究T22次列车的长度与速度,记录了以下两个数据:
青藏铁路于2006年7月1日胜利通车,青藏高原天堑变通途,圆了几代人的梦想.作为世界上海拔最高,施工难度最大的铁路,青藏铁路全县有一座大桥-拉萨河大桥(如图)全长920多米,其中主桥长800米,小明在去年暑假乘T22次列车从北京到拉萨游玩,小明为了探究T22次列车的长度与速度,记录了以下两个数据: