题目内容
15.双曲线y=$\frac{k}{x}$和直线y=x+1交于点(-2,m),则双曲线的表达式为y=$\frac{2}{x}$.分析 先由一次函数的解析式确定点的坐标,再把点的坐标代入反比例函数的解析式即可.
解答 解:把点(-2,m)代入y=x+1得:m=-2+1=-1,
∴点(-2,-1),
把点(-2,-1)代入y=$\frac{k}{x}$得,k=2,
∴双曲线的表达式为y=$\frac{2}{x}$.
故答案为:y=$\frac{2}{x}$.
点评 本题考查了由函数的解析式确定点的坐标,待定系数法确定函数的解析式,注意知识的综合运用.

练习册系列答案
相关题目
3.在平面直角坐标系xOy中,对于点P(x,y),我们把点P(-y+1,x+1)叫做点P的伴随点.已知点A1的伴随点为A2,点A2的伴随点为A3,点A3的伴随点为A4,…,这样依次得到点A1,A2,A3,…,An,….例如:点A1的坐标为(3,1),则点A2的坐标为(0,4),…;若点A1的坐标为(a,b),则点A2015的坐标为( )
| A. | (-b+1,a+1) | B. | (-a,-b+2) | C. | (b-1,-a+1) | D. | (a,b) |
20.下列计算正确的是( )
| A. | a4+a4=a8 | B. | (a3)4=a7 | ||
| C. | 12a6b4÷3a2b-2=4a4b2 | D. | (-a3b)2=a6b2 |
5.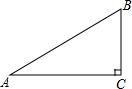 如图,在△ABC中,∠C=90°,AB=5,BC=3,则cosA的值是( )
如图,在△ABC中,∠C=90°,AB=5,BC=3,则cosA的值是( )
 如图,在△ABC中,∠C=90°,AB=5,BC=3,则cosA的值是( )
如图,在△ABC中,∠C=90°,AB=5,BC=3,则cosA的值是( )| A. | $\frac{3}{4}$ | B. | $\frac{4}{3}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
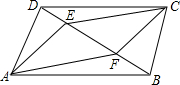 如图,己知AB∥DC,且AB=CD,BF=DE,说明AE∥CF,AF∥CE的理由.
如图,己知AB∥DC,且AB=CD,BF=DE,说明AE∥CF,AF∥CE的理由.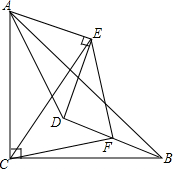 如图,△ABC、△ADE为等腰直角三角形,∠ACB=∠AED=90°.连接BD,取BD中点F,连接CF,EF,CE.求证:△CEF为等腰直角三角形.
如图,△ABC、△ADE为等腰直角三角形,∠ACB=∠AED=90°.连接BD,取BD中点F,连接CF,EF,CE.求证:△CEF为等腰直角三角形.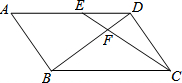 如图,在?ABCD中,点E在AD上,若DE=6,S△DEF:S△BCF=4:25,则AE=9.
如图,在?ABCD中,点E在AD上,若DE=6,S△DEF:S△BCF=4:25,则AE=9.