题目内容
13.(1)计算:$\sqrt{3}$(1-$\sqrt{3}$)+$\sqrt{12}$+($\frac{1}{3}$)-1;(2)解方程:$\frac{x}{x+1}$=$\frac{2x}{3x+3}$+1.
(3)当x=$\sqrt{2}$-1时,求代数式$\frac{{x}^{2}-2x+1}{x+1}$÷$\frac{x-1}{{x}^{2}+x}$+x的值.
(4)当m取何值时,关于x的分式方程$\frac{2}{x-2}$+$\frac{mx}{{x}^{2}-4}$=$\frac{3}{x+2}$产生增根?
分析 (1)原式第一项利用二次根式乘法法则计算,第二项化为最简二次根式,第三项利用负整数指数幂法则计算即可得到结果;
(2)分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解;
(3)原式第一项利用除法法则变形,约分后计算得到最简结果,把x的值代入计算即可求出值;
(4)分式方程去分母转化为整式方程,由分式方程有增根,得到最简公分母为0,求出x的值,代入整式方程即可求出m的值.
解答 解:(1)原式=$\sqrt{3}$-3+2$\sqrt{3}$+3=3$\sqrt{3}$;
(2)去分母得,3x=2x+3x+3,
解得:x=-$\frac{3}{2}$,
经检验:原方程的根是x=-$\frac{3}{2}$;
(3)原式=$\frac{(x-1)^{2}}{x+1}$•$\frac{x(x+1)}{x-1}$+x=x(x-1)+x=x2,
当x=$\sqrt{2}$-1时,原式=($\sqrt{2}$-1)2=3-2$\sqrt{2}$;
(4)原方程可化为,2x+4+mx=3x-6,即(1-m)x=10,
当x=2时,1-m=5,解得m=-4;当x=-2时,1-m=-5,解得m=6,
因此当m=-4或6时,原分式方程会产生增根.
点评 此题考查了分式的化简求值,熟练掌握运算法则是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8.若两个相似三角形的面积之比为1:4,则它们的周长之比为( )
| A. | 1:2 | B. | 2:1 | C. | 1:4 | D. | 4:1 |
3.已知二次函数y=$\frac{1}{2}$(x+3)2+5,则此图象的顶点坐标为( )
| A. | (3,5) | B. | (-3,-5) | C. | (-3,5) | D. | (3,-5) |
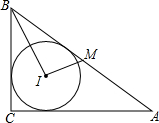 在Rt△ABC中,∠C是直角,M是AB中点,I是内心,若BI⊥IM,求BC:AC.
在Rt△ABC中,∠C是直角,M是AB中点,I是内心,若BI⊥IM,求BC:AC.