题目内容
4.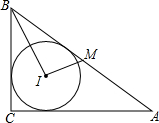 在Rt△ABC中,∠C是直角,M是AB中点,I是内心,若BI⊥IM,求BC:AC.
在Rt△ABC中,∠C是直角,M是AB中点,I是内心,若BI⊥IM,求BC:AC.
分析 延长MI角BC于N,作MH⊥BC于H,作ID⊥AB于D,IE⊥BC于E,如图,设BC=a,AC=b,⊙I的半径为r,根据三角形内切圆的性质和内心的性质得IE=ID=r,IB平分∠MBN,而BI⊥IM,则可判断△AMN为等腰三角形,则可利用面积法得到MH=IE+ID=2r,再证明MH为△ABC的中位线得到MH=$\frac{1}{2}$b,根据直角三角形的内切圆半径与三边的关系得r=$\frac{a+b-AB}{2}$,即a+b-AB=$\frac{1}{2}$b,于是得到AB=a+$\frac{1}{2}$b,然后利用勾股定理得到(a+$\frac{1}{2}$b)2=a2+b2,再整理即可得到a与b的值.
解答 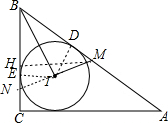 解:延长MI角BC于N,作MH⊥BC于H,作ID⊥AB于D,IE⊥BC于E,如图,
解:延长MI角BC于N,作MH⊥BC于H,作ID⊥AB于D,IE⊥BC于E,如图,
设BC=a,AC=b,⊙I的半径为r,
∵I是内心,
∴IE=ID=r,IB平分∠MBN,
∵BI⊥IM,
∴△AMN为等腰三角形,
∴MH=IE+ID=2r,
∵M是AB中点,
∴MH为△ABC的中位线,
∴MH=$\frac{1}{2}$b,
而r=$\frac{a+b-AB}{2}$,
∴a+b-AB=$\frac{1}{2}$b,
∴AB=a+$\frac{1}{2}$b,
∵AB2=a2+b2,
∴(a+$\frac{1}{2}$b)2=a2+b2,
整理得4a-3b=0,
∴$\frac{a}{b}$=$\frac{3}{4}$,
即BC:AC=3:4.
点评 本题考查了三角形的内切圆与内心:与三角形各边都相切的圆叫三角形的内切圆,三角形的内切圆的圆心叫做三角形的内心,这个三角形叫做圆的外切三角形.三角形的内心就是三角形三个内角角平分线的交点.记住直角三角形的内切圆半径与三边的关系(r=$\frac{a+b-c}{2}$,a、b为直角边,c为斜边).

 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案| A. | k>$\frac{1}{2}$或k≠1 | B. | k>$\frac{1}{2}$且k≠1 | C. | k<$\frac{1}{2}$且k≠1 | D. | k<$\frac{1}{2}$或k≠1 |
| A. | (2x+3y)(2x-3y)=2x2-3y2 | B. | (-4b2+a)(4b2-a)=16b4-a2 | ||
| C. | (x-2)(2+x)=4-x2 | D. | (-ab-c)(c-ab)=a2b2-c2 |
| A. | -5 | B. | -1 | C. | 1 | D. | 5 |
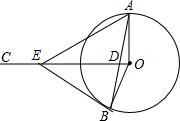 如图,OA、OB是⊙O的半径,过点O作OC⊥OA,交弦AB于点D,点E是BD的垂直平分线与OC的交点,连接BE
如图,OA、OB是⊙O的半径,过点O作OC⊥OA,交弦AB于点D,点E是BD的垂直平分线与OC的交点,连接BE
 如图,如果一个平行四边形的对角线长分别为8和6,那么这个平行四边形的边长m的取值范围是1<m<7.
如图,如果一个平行四边形的对角线长分别为8和6,那么这个平行四边形的边长m的取值范围是1<m<7.