题目内容
11.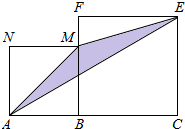 如图,线段AC=n+1(其中n为正整数),点B在线段AC上,在线段AC同侧作正方形ABMN及正方形BCEF,连接AM、ME、EA得到△AME.当AB=1时,△AME的面积记为S1;当AB=2时,△AME的面积记为S2;当AB=3时,△AME的面积记为S3;…;当AB=n时,△AME的面积记为Sn,则Sn=$\frac{1}{2}$n2.(用含n的代数式表示)
如图,线段AC=n+1(其中n为正整数),点B在线段AC上,在线段AC同侧作正方形ABMN及正方形BCEF,连接AM、ME、EA得到△AME.当AB=1时,△AME的面积记为S1;当AB=2时,△AME的面积记为S2;当AB=3时,△AME的面积记为S3;…;当AB=n时,△AME的面积记为Sn,则Sn=$\frac{1}{2}$n2.(用含n的代数式表示)
分析 根据连接BE,则BE∥AM,利用△AME的面积=△AMB的面积即可得出Sn=$\frac{1}{2}$n2.
解答 解:连接BE.
∵在线段AC同侧作正方形ABMN及正方形BCEF,
∴BE∥AM,
∴△AME与△AMB同底等高,
∴△AME的面积=△AMB的面积,
∴当AB=n时,△AME的面积记为Sn=$\frac{1}{2}$n2,
故答案为:$\frac{1}{2}$n2
点评 此题主要考查了三角形面积求法以及正方形的性质,根据已知得出正确图形,得出S与n的关系是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.过⊙O内一点N的最长弦为6,最短的弦长为4,那么ON的长为( )
| A. | $\sqrt{3}$ | B. | 2 | C. | $\sqrt{5}$ | D. | $\sqrt{3}$ |
20.已知关于x的一元二次方程x2-ax-1=0(其中a为常数)的根的情况是( )
| A. | 有两个不相等的实数根 | B. | 可能有实数根,也可能没有实数根 | ||
| C. | 有两个不相等的实数根 | D. | 没有实数根 |
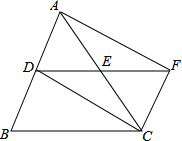 如图,△ABC中,DE是一条中位线,延长DE到点F,使EF=DE,连接CF.
如图,△ABC中,DE是一条中位线,延长DE到点F,使EF=DE,连接CF. 先观察图形,再用所学的知识验证直线a,b是否平行.
先观察图形,再用所学的知识验证直线a,b是否平行.