题目内容
12.已知m与n是方程2x2-6x+3=0的两根.(1)填空:m+n=3,m•n=$\frac{3}{2}$;
(2)计算$\frac{1}{m}$+$\frac{1}{n}$的值.
分析 (1)由根与系数的关系即可得出m+n=3,m•n=$\frac{3}{2}$,由此即可得出结论;
(2)将$\frac{1}{m}$+$\frac{1}{n}$转化成只含m+n和mn的形式,代入数据即可得出结论.
解答 解:(1)∵m与n是方程2x2-6x+3=0的两根,
∴m+n=-$\frac{-6}{2}$=3,m•n=$\frac{3}{2}$,
故答案为:3;$\frac{3}{2}$.
(2)$\frac{1}{m}$+$\frac{1}{n}$=$\frac{m+n}{mn}$=$\frac{3}{\frac{3}{2}}$=2.
点评 本题考查了根与系数的关系,解题的关键是:(1)根据根与系数的关系得出m+n=-$\frac{-6}{2}$=3,m•n=$\frac{3}{2}$;(2)将$\frac{1}{m}$+$\frac{1}{n}$变形为$\frac{m+n}{mn}$.本题属于基础题,难度不大,解决该题型题目时,根据根与系数的关系得出两根之和与两根之积是关键.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
2.用反证法证明“a∥b,b∥c,则a∥c”时,第一步应先假设( )
| A. | a不平行于c | B. | b不平行于c | C. | a⊥c | D. | b⊥c |
 如图,在?ABCD中,已知点E和点F分别在AD和BC上,且AE=CF,连结CE和AF,试说明四边形AFCE是平行四边形.
如图,在?ABCD中,已知点E和点F分别在AD和BC上,且AE=CF,连结CE和AF,试说明四边形AFCE是平行四边形.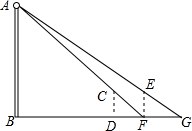 如图,河对岸有一路灯杆AB,在灯光下,小明在点D处测得自己的影长DF=3m,沿BD方向到达点F处再测得自己的影长FG=4m.如果小明的身高为1.7m,求路灯杆AB的高度.
如图,河对岸有一路灯杆AB,在灯光下,小明在点D处测得自己的影长DF=3m,沿BD方向到达点F处再测得自己的影长FG=4m.如果小明的身高为1.7m,求路灯杆AB的高度.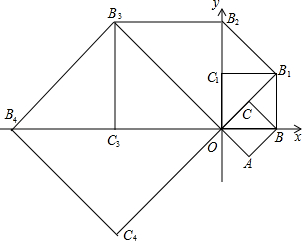 如图,在平面直角坐标系xOy中,有一边为1的正方形OABC,点B在x轴的正半轴上,如果以对角线OB为边作第二个正方形OBB1C1,再以对角线OB1为边作第三个正方形OB1B2C2,…,照此规律作下去,则B2的坐标是(0,2$\sqrt{2}$);B2015的坐标是(${2}^{254}\sqrt{2}$,-${2}^{254}\sqrt{2}$).
如图,在平面直角坐标系xOy中,有一边为1的正方形OABC,点B在x轴的正半轴上,如果以对角线OB为边作第二个正方形OBB1C1,再以对角线OB1为边作第三个正方形OB1B2C2,…,照此规律作下去,则B2的坐标是(0,2$\sqrt{2}$);B2015的坐标是(${2}^{254}\sqrt{2}$,-${2}^{254}\sqrt{2}$). 在△ABC中,∠C=90°,AC=6,BC=8,AB=10,点D在BC上,将△ACD沿AD对折,点C刚好落在AB上的E点,求CD的长.
在△ABC中,∠C=90°,AC=6,BC=8,AB=10,点D在BC上,将△ACD沿AD对折,点C刚好落在AB上的E点,求CD的长. 在平面直角坐标系中,△ABC的三个顶点的横、纵坐标均为整数,点A′的坐标是(-4,0),现将△ABC平移.使点A平移到点A′,点B′、C分别是B、C的对应点.
在平面直角坐标系中,△ABC的三个顶点的横、纵坐标均为整数,点A′的坐标是(-4,0),现将△ABC平移.使点A平移到点A′,点B′、C分别是B、C的对应点. 如图,在△ABC中,∠C=90°,∠EAB,∠ABD是△ABC的外角,AF,BF分别平分∠EAB及∠ABD,求证:∠AFB=45°.
如图,在△ABC中,∠C=90°,∠EAB,∠ABD是△ABC的外角,AF,BF分别平分∠EAB及∠ABD,求证:∠AFB=45°.