Question

20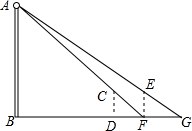．如图，河对岸有一路灯杆AB，在灯光下，小明在点D处测得自己的影长DF=3m，沿BD方向到达点F处再测得自己的影长FG=4m．如果小明的身高为1.7m，求路灯杆AB的高度．

Answer 1

分析 根据相似三角形的判定与性质分别得出比例式，进而利用BD，AB的长．

解答 解：∵AB∥CD，
∴△ABF∽△CDF，
∴$\frac{AB}{CD}$=$\frac{BF}{DF}$，
即$\frac{AB}{1.7}$=$\frac{3+DB}{3}$，
∵AB∥EF，
∴△ABG∽△EFG，
∴$\frac{AB}{EF}$=$\frac{BG}{FG}$，
即$\frac{AB}{1.7}$=$\frac{BD+7}{4}$，
∵CD=EF，
∴$\frac{3+BD}{3}$=$\frac{7+BD}{4}$，
解得：BD=9（m），
把BD=9代入$\frac{AB}{1.7}$=$\frac{3+9}{3}$，
解得：AB=6.8m，
答：路灯AB的高度为6.8m．

点评 此题主要考查了相似三角形的应用，正确得出BD的长是解题关键．