题目内容
15.2014年杭州市推出了“微公交”,“微公交”是国内首创的纯电动汽车租赁服务,它作为一种绿色出行方式,对缓解交通堵塞和停车困难,改善城市大气环境,都可以起到积极作用,据了解某租赁点用有“微公交”20辆,据统计,当每辆车的年租金为9千元时可全部租出,每辆车的年租金每增加0.5千元,未租出的车将增加1辆.(1)当每辆车的年租金定为10.5千元时,能租出多少辆?
(2)当每辆车的年租金增加多少元时,租赁公司的年收益(不计车辆维护等其它费用)可达到176千元?
分析 (1)10.5-9=1.5,由题意得,当租金为10.5千元时有3辆没有租出;
(2)设每辆车的年租金增加x千元时,直接根据收益=176千元作为等量关系列方程求解即可.
解答 解:(1)由题意:当每辆车的年租金每增加0.5千元时,未租出的车将增加一辆,
则当每辆车的年租金定为10.5千元时,10.5-9=1.5(元),
所以1.5÷0.5=3(辆).
所以该公司有3辆没有租出,即共租出17辆.
(2)设每辆车的年租金增加x千元时,租赁公司年收益为176千元,由题意,得
(9+x)×(20-2x)=176,
整理,得(x-2)(x+1)=0,
解得x=2或x=-1(舍去).
答:当每辆车的年租金增加2000元时,租赁公司的年收益(不计车辆维护等其它费用)可达到176千元.
点评 本题考查了一元二次方程的应用,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系是解题关键.

练习册系列答案
相关题目
5.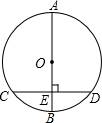 如图,AB为⊙O的直径,弦CD垂直平分半径OB,垂足为E,CD=6cm,则直径AB的长是( )
如图,AB为⊙O的直径,弦CD垂直平分半径OB,垂足为E,CD=6cm,则直径AB的长是( )
 如图,AB为⊙O的直径,弦CD垂直平分半径OB,垂足为E,CD=6cm,则直径AB的长是( )
如图,AB为⊙O的直径,弦CD垂直平分半径OB,垂足为E,CD=6cm,则直径AB的长是( )| A. | 10cm | B. | 3$\sqrt{2}$cm | C. | 4$\sqrt{2}$cm | D. | 4$\sqrt{3}$cm |
6.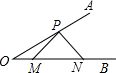 如图,已知∠AOB=30°,点P在边OA上,OP=4,点M,N在边OB上,PM=PN,且∠MPN=90°,则ON=( )
如图,已知∠AOB=30°,点P在边OA上,OP=4,点M,N在边OB上,PM=PN,且∠MPN=90°,则ON=( )
 如图,已知∠AOB=30°,点P在边OA上,OP=4,点M,N在边OB上,PM=PN,且∠MPN=90°,则ON=( )
如图,已知∠AOB=30°,点P在边OA上,OP=4,点M,N在边OB上,PM=PN,且∠MPN=90°,则ON=( )| A. | 8 | B. | 6 | C. | 2$\sqrt{3}$+4 | D. | 2$\sqrt{3}$+2 |
3.下列等式成立的是( )
| A. | $\sqrt{7}$-$\sqrt{2}$=$\sqrt{5}$ | B. | $\sqrt{2}$×$\sqrt{3}$=$\sqrt{6}$ | C. | $\sqrt{{2}^{2}+{3}^{2}}$=5 | D. | -$\sqrt{(-5)^{2}}$=5 |
20.计算(2ab2)3,结果正确的是( )
| A. | 2a3b6 | B. | 6a3b6 | C. | 8a3b5 | D. | 8a3b6 |
7.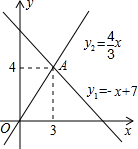 如图,一次函数y1=-x+7与正比例函数y2=$\frac{4}{3}$x的图象交于点A,若y1>y2,则自变量x的取值范围是( )
如图,一次函数y1=-x+7与正比例函数y2=$\frac{4}{3}$x的图象交于点A,若y1>y2,则自变量x的取值范围是( )
 如图,一次函数y1=-x+7与正比例函数y2=$\frac{4}{3}$x的图象交于点A,若y1>y2,则自变量x的取值范围是( )
如图,一次函数y1=-x+7与正比例函数y2=$\frac{4}{3}$x的图象交于点A,若y1>y2,则自变量x的取值范围是( )| A. | x>3 | B. | x<3 | C. | x>4 | D. | x<4 |