题目内容
9.已知数轴上,点O为原点,点A对应的数为11,点B对应的数为b,点C在点B右侧,长度为3个单位的线段BC在数轴上移动,(1)如图1,当线段BC在O,A两点之间移动到某一位置时,恰好满足线段AC=OB,求此时b的值;
(2)线段BC在数轴上沿射线AO方向移动的过程中,是否存在AC-OB=$\frac{1}{2}$AB?若存在,求此时满足条件的b的值;若不存在,说明理由.
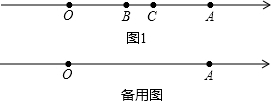
分析 (1)由题意可知B点表示的数比点C对应的数少3,进一步用b表示出AC、OB之间的距离,联立方程求得b的数值即可;
(2)分别用b表示出AC、OB、AB,进一步利用AC-0B=$\frac{1}{2}$AB建立方程求得答案即可.
解答 解:(1)由题意得:
11-(b+3)=b,
解得:b=4.
答:线段AC=OB,此时b的值是4.
(2)由题意得:
①11-(b+3)-b=$\frac{1}{2}$(11-b),
解得:b=$\frac{5}{3}$.
②11-(b+3)+b=$\frac{1}{2}$(11-b),
解得:b=-5.
答:若AC-0B=$\frac{1}{2}$AB,满足条件的b值是$\frac{5}{3}$或-5.
点评 本题考查了一元一次方程的应用,考查了数轴与两点间的距离的计算,根据数轴确定出线段的长度是解题的关键.

练习册系列答案
 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案
相关题目
20.下列属于一元一次方程的是( )
| A. | x+1 | B. | 3x+2x=2 | C. | 5x-5=4y-4 | D. | x2-2x+1=0 |
17.小强是一位密码编译爱好者,在他的密码手册中,有这样一条信息:a-b,x-y,x+y,a+b,x2-y2,a2-b2分别对应下列六个字:华、爱、我、中、游、美,现将(x2-y2)a2-(x2-y2)b2因式分解,结果呈现的密码信息可能是( )
| A. | 我爱美 | B. | 中华游 | C. | 爱我中华 | D. | 美我中华 |
4.在解方程$\frac{x-1}{2}$$-\frac{2x+3}{3}$=1时,去分母正确的是( )
| A. | (x-1)-2(2+3x)=13 | B. | (x-1)+2(2x+3)=1 | C. | 3(x-1)+2(2+3x)=6 | D. | 3(x-1)-2(2x+3)=6 |
14.下面计算正确的是( )
| A. | $\sqrt{27}$÷$\sqrt{3}$=3 | B. | 3+$\sqrt{3}$=3$\sqrt{3}$ | C. | $\sqrt{2}$•$\sqrt{3}$=$\sqrt{5}$ | D. | $\sqrt{(-2)^{2}}$=-2 |
18.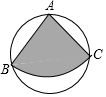 如图,从直径是2米的圆形铁皮上剪出一个圆心角是90°的扇形ABC(A,B,C三点在⊙O上),将剪下来的扇形围成一个圆锥的侧面,则该圆锥的底面圆的半径为( )
如图,从直径是2米的圆形铁皮上剪出一个圆心角是90°的扇形ABC(A,B,C三点在⊙O上),将剪下来的扇形围成一个圆锥的侧面,则该圆锥的底面圆的半径为( )
 如图,从直径是2米的圆形铁皮上剪出一个圆心角是90°的扇形ABC(A,B,C三点在⊙O上),将剪下来的扇形围成一个圆锥的侧面,则该圆锥的底面圆的半径为( )
如图,从直径是2米的圆形铁皮上剪出一个圆心角是90°的扇形ABC(A,B,C三点在⊙O上),将剪下来的扇形围成一个圆锥的侧面,则该圆锥的底面圆的半径为( )| A. | 4-$\frac{π}{9}$ | B. | $\frac{\sqrt{2}}{4}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\sqrt{2}$ |
19.下列说法中,正确的是( )
| A. | 为检测市场上正在销售的酸奶质量,应该采用全面调查的方式 | |
| B. | 在连续5次的数学测试中,两名同学的平均分相同,方差较大的同学数学成绩更稳定 | |
| C. | 小强班上有3个同学都是16岁,因此小强认为他们班学生年龄的众数是16岁 | |
| D. | 给定一组数据,则这组数据的中位数一定只有一个 |
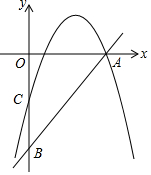 如图,直线y=2x-10分别与x轴,y轴交于点A,B,点C为OB的中点,抛物线y=-x2+bx+c经过A,C两点.
如图,直线y=2x-10分别与x轴,y轴交于点A,B,点C为OB的中点,抛物线y=-x2+bx+c经过A,C两点.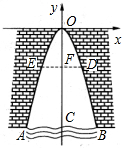 某涵洞的截面边缘成抛物线形,现测得当水面宽AB=2米时涵洞的顶点与水面的距离为4米,这时离开水面2米处涵洞宽DE是多少?
某涵洞的截面边缘成抛物线形,现测得当水面宽AB=2米时涵洞的顶点与水面的距离为4米,这时离开水面2米处涵洞宽DE是多少?