题目内容
求证:等腰三角形底边中线上任意一点到两腰的距离相等.
(1)根据题意画出图形,并写出已知和求证;
(2)证明结论.
(1)根据题意画出图形,并写出已知和求证;
(2)证明结论.
考点:等腰三角形的性质
专题:
分析:根据题意画出图形,写出已知与求证,然后证明:由AB=AC,D为BC中点,利用等腰三角形的“三线合一”性质得到AD为顶角的平分线,根据角平分线上的点到角两边的距离相等即可得到DE=DF得证.
解答: 解:(1)已知:在△ABC中,AB=AC,AD为BC边上的中线,P为AD上的任一点,PE⊥AB,PF⊥AC,
解:(1)已知:在△ABC中,AB=AC,AD为BC边上的中线,P为AD上的任一点,PE⊥AB,PF⊥AC,
求证:PE=PF;
(2)证明:∵AB=AC,AD为BC边上的中线,
∴AD平分∠BAC,
∵PE⊥AB,PF⊥AC,
∴PE=PF.
 解:(1)已知:在△ABC中,AB=AC,AD为BC边上的中线,P为AD上的任一点,PE⊥AB,PF⊥AC,
解:(1)已知:在△ABC中,AB=AC,AD为BC边上的中线,P为AD上的任一点,PE⊥AB,PF⊥AC,求证:PE=PF;
(2)证明:∵AB=AC,AD为BC边上的中线,
∴AD平分∠BAC,
∵PE⊥AB,PF⊥AC,
∴PE=PF.
点评:本题主要考查等腰三角形的性质的应用,关键是掌握等腰三角形的腰相等且底边上的两个角相等,及角平分线上的点到角两边的距离相等.

练习册系列答案
相关题目

 如图,长方体的长为6,宽、高均为4,一只蚂蚁从A处沿长方体表面爬到B处的最短路程等于
如图,长方体的长为6,宽、高均为4,一只蚂蚁从A处沿长方体表面爬到B处的最短路程等于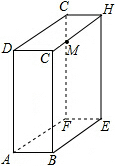 如图,长方体的长BE=15cm,宽AB=10cm,高AD=20cm,点M在CH上,且CM=5cm,一只蚂蚁如果要沿着长方体的表面从点A爬到点M,需要爬行的最短距离是多少?
如图,长方体的长BE=15cm,宽AB=10cm,高AD=20cm,点M在CH上,且CM=5cm,一只蚂蚁如果要沿着长方体的表面从点A爬到点M,需要爬行的最短距离是多少?