Question

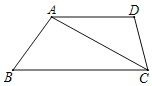
【题目】如图，在菱形ABCD中，∠ADE、∠CDF分别交BC、AB于点E、F，DF交对角线AC于点M，且∠ADE＝∠CDF．

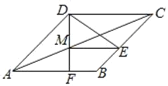
（1）求证：CE＝AF；

（2）连接ME，若＝，AF＝2，求的长．

Answer 1

【答案】（1）见解析（2）2

【解析】

（1）通过已知条件，易证△ADF≌△CDE，即可求得；

（2）根据＝，易求得BE和BF，根据已知条件可得＝＝，证明△AMF∽△CMD，，再证明△ABC～△MEC,即可求出ME．

解：（1）∵四边形ABCD是菱形，

∴AD＝CD，∠DAF＝∠DCE，

又∵∠ADE＝∠CDF，

∴∠ADE﹣∠EDF＝∠CDF﹣∠EDF，

∴∠ADF＝∠CDE，

在△ADF和△CDE中，

，

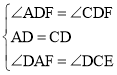∴△ADF≌△CDE，

∴CE＝AF．

（2）∵四边形ABCD是菱形，

∴AB＝BC，

由（1）得：CE＝AF＝2，

∴BE＝BF，

设BE＝BF＝x，

∵＝，AF＝2，

∴，解得x＝，

∴BE＝BF＝，

∵＝，且CE＝AF，

∴＝＝，

∵∠CMD＝∠AMF，∠DCM＝∠AMF，

∴△AMF∽△CMD，

∴，

∴，且∠ACB＝∠ACB,

∴△ABC～△MEC,

∴∠CAB＝∠CME=∠ACB，

∴ME=CE=2．