Question

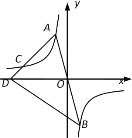
【题目】如图，点A，B，C在反比例函数的图象上，且直线AB经过原点，点C在第二象限上，连接AC并延长交x轴于点D，连接BD，若△BOD的面积为9，则=_____．

Answer 1

【答案】

【解析】

过点A作AN⊥x轴于N，过点C作CM⊥x轴于M，则CM∥AN，设出A点坐标，B点与A点对称，可得B点坐标，进而可得直线AB解析式，联立反比例函数，可得A，C两点坐标，根据平行线分线段成比例可得出答案.

过点A作AN⊥x轴于N，过点C作CM⊥x轴于M，则CM∥AN，如图：

∵A点在反比例函数的图象上，

∴设A点坐标为（a，-），

∵直线AB经过原点，A，B两点在反比例函数的图象上，

∴A，B两点关于原点对称，

∴B点（-a，），

∴S△BOD=×OD×(-)=9，

∴OD=-，∴D（，0），

设直线AD的解析式为y=kx+b，

∴ ，解得，

∴直线AD的解析式为，

将直线AD的解析式与反比例函数的解析式联立，组成方程组， ，

解得 或 ，

∴C点坐标为（，-），A（a，-），

又∵D（a，0），

∴DM==-a，MN=a-=-，

∵CM∥AN，

∴

故答案为；.