题目内容
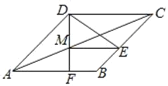
【题目】如图,在四边形ABCD中,AD∥BC.
(1)求作直线EF使得EF交AD于点E,交BC于点F且使得EA=EC,FA=FC(尺规作图,保留作图痕迹,不写作法);
(2)连接AF、CE,判断四边形AFCE的形状,并说明理由.
【答案】(1)见解析;(2)四边形AFCE为菱形.理由见解析;
【解析】
(1)作线段AC的垂直平分线交AD于E,交BC于F,连接EC,AF即可.
(2)根据四边相等的四边形是菱形证明即可.
(1)作线段AC的垂直平分线交AD于E,交BC于F,连接EC,AF即可.
(2)根据四边相等的四边形是菱形证明即可.
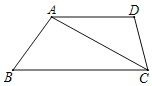
解:(1)如图,点E、F为所作.

(2)四边形AFCE为菱形.理由如下:
∵EF垂直平分AC,
∴AE=CE,AF=CF,
∴EF平分∠AFC,即∠AFE=∠CFE,
∵AD∥BC,
∴∠AEF=∠CFE,
∴∠AFE=∠AEF,
∴AE=AF,
∴AE=EC=CF=AF,
∴四边形AFCE为菱形.

 阅读快车系列答案
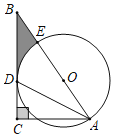
阅读快车系列答案【题目】如图,Rt△ABC中,∠ACB=90°,AD平分∠BAC交BC于点D,点O为AB上一点,以O为圆心,AO为半径的圆经过点D.
(1)求证:BC与⊙O相切;
(2)若BD=AD=![]() ,求阴影部分的面积.
,求阴影部分的面积.
【题目】![]() 年新冠肺炎疫情发生以来,每天测体温成为一种制度,手持红外测温枪成为紧俏商品.某经销店承诺对所有商品明码标价,绝不哄抬物价.如下表所示是该店甲、乙两种手持红外测温枪的进价和售价:
年新冠肺炎疫情发生以来,每天测体温成为一种制度,手持红外测温枪成为紧俏商品.某经销店承诺对所有商品明码标价,绝不哄抬物价.如下表所示是该店甲、乙两种手持红外测温枪的进价和售价:
商品 价格 | 甲 | 乙 |
进件(元 |
|
|
售价(元 |
|
|
该店有一批用![]() 元购进的甲、乙两种手持红外测温枪库存,预计全部销售后可获毛利润共
元购进的甲、乙两种手持红外测温枪库存,预计全部销售后可获毛利润共![]() 元.[毛利润
元.[毛利润![]() (售价
(售价![]() 进价)
进价)![]() 销售量]
销售量]


(1)该店库存的甲、乙两种手持红外测温枪分别为多少个?
(2)根据销售情况,该店计划增加甲种手持红外测温枪的购进量,减少乙种手持红外测温枪的购进量.已知甲种手持红外测温枪增加的数量是乙种手持红外测温枪减少的数量的![]() 倍,进货价不变,而且用于购进这两种手持红外测温枪的总资金不超过
倍,进货价不变,而且用于购进这两种手持红外测温枪的总资金不超过![]() 元,则该店怎样进货,可使全部销售后获得的毛利润最大?并求出最大毛利润.
元,则该店怎样进货,可使全部销售后获得的毛利润最大?并求出最大毛利润.