题目内容
 如图1,在四边形ABCD的边AB上任取一点E(点E不与点A、点B重合),分别连接ED,EC,可以把四边形ABCD分成三个三角形,如果其中有两个三角形相似,我们就把E叫做四边形ABCD的边AB上的相似点;如果这三个三角形都相似,我们就把E叫做四边形ABCD的边AB上的强相似点.
如图1,在四边形ABCD的边AB上任取一点E(点E不与点A、点B重合),分别连接ED,EC,可以把四边形ABCD分成三个三角形,如果其中有两个三角形相似,我们就把E叫做四边形ABCD的边AB上的相似点;如果这三个三角形都相似,我们就把E叫做四边形ABCD的边AB上的强相似点.(1)如图2,画出矩形ABCD中的AB边上的一个强相似点.(要求:画图工具不限,不写画法,保留画图痕迹或有必要说明).
(2)对于任意的一个矩形,是否一定存在强相似点?如果一定存在,请说明理由;如果不一定存在,请举出反例.
考点:作图—相似变换
专题:
分析:(1)以CD为直径画弧,取该弧与AB的一个交点即为所求;
(2)根据(1)的作法,若矩形的宽大于长的一半,则圆与另一边没有交点,也就不存在全相似点.
(2)根据(1)的作法,若矩形的宽大于长的一半,则圆与另一边没有交点,也就不存在全相似点.
解答:解:(1)如图所示:点E是四边形ABCD的边AB上的相似点,
 ;
;
(2)由(1)可知,当矩形的长AB<2AD时,圆与AB没有交点,所以AB边上不存在这样的全相似点E.
(答案不惟一,若学生画图说明也可.)
 ;
;(2)由(1)可知,当矩形的长AB<2AD时,圆与AB没有交点,所以AB边上不存在这样的全相似点E.
(答案不惟一,若学生画图说明也可.)
点评:本题是相似三角形综合题,主要考查了相似三角形的对应边成比例的性质,读懂题目信息,理解全相似点的定义,判断出∠CED=90°,从而确定作以CD为直径的圆是解题的关键.

练习册系列答案
相关题目
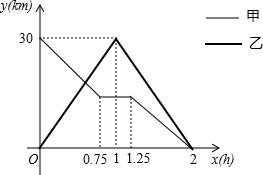 在一条笔直的公路上有A、B两地.甲、乙两人同时出发,甲骑电动车从A地到B地,中途出现故障后停车维修,修好车后以原速继续行驶到B地;乙骑摩托车从B地到A地,到达A地后立即按原路原速返回,结果两人同时到B地.如图是甲、乙两人与B地的距离y(km)与乙行驶时间x(h)之间的函数图象.
在一条笔直的公路上有A、B两地.甲、乙两人同时出发,甲骑电动车从A地到B地,中途出现故障后停车维修,修好车后以原速继续行驶到B地;乙骑摩托车从B地到A地,到达A地后立即按原路原速返回,结果两人同时到B地.如图是甲、乙两人与B地的距离y(km)与乙行驶时间x(h)之间的函数图象.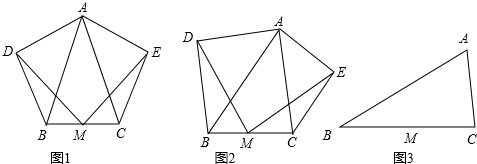
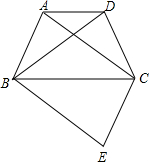 如图,四边形ABCD为等腰梯形,AD∥BC,连结AC、BD.在平面内将△DBC沿BC翻折得到△EBC.
如图,四边形ABCD为等腰梯形,AD∥BC,连结AC、BD.在平面内将△DBC沿BC翻折得到△EBC.
 如图,在平面直角坐标系xOy中,已知抛物线y=-x(x-3)(0≤x≤3)在x轴上方的部分,记作C1,它与x轴交于点O,A1,将C1绕点A1旋转180°得C2,C2与x 轴交于另一点A2.请继续操作并探究:将C2绕点A2旋转180°得C3,与x轴交于另一点A3;将C3绕点A2旋转180°得C4,与x轴交于另一点A4,这样依次得到x轴上的点A1,A2,A3,…,An,…,及抛物线C1,C2,…,Cn,….则点A4的坐标为
如图,在平面直角坐标系xOy中,已知抛物线y=-x(x-3)(0≤x≤3)在x轴上方的部分,记作C1,它与x轴交于点O,A1,将C1绕点A1旋转180°得C2,C2与x 轴交于另一点A2.请继续操作并探究:将C2绕点A2旋转180°得C3,与x轴交于另一点A3;将C3绕点A2旋转180°得C4,与x轴交于另一点A4,这样依次得到x轴上的点A1,A2,A3,…,An,…,及抛物线C1,C2,…,Cn,….则点A4的坐标为