题目内容
如图:抛物线y=-x2+bx+c交x轴于A、B,直线y=x+2过点A,交y轴于C,交抛物线于D,且D的纵坐标为5.
(1)求抛物线解析式;
(2)点P为抛物线第一象限的图象上的一点,直线PC交x轴于点E,若PC=3CE,求点P的坐标;
(3)在(2)的条件下,点Q为x轴上一点,把△PCQ沿CQ翻折,点P刚好落在x轴上点G处,求Q点的坐标.
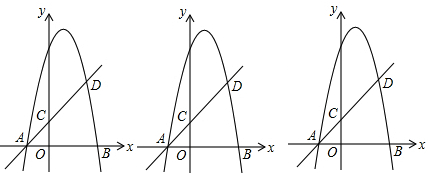
(1)求抛物线解析式;
(2)点P为抛物线第一象限的图象上的一点,直线PC交x轴于点E,若PC=3CE,求点P的坐标;
(3)在(2)的条件下,点Q为x轴上一点,把△PCQ沿CQ翻折,点P刚好落在x轴上点G处,求Q点的坐标.

考点:二次函数综合题
专题:
分析:(1)将已知点的坐标代入二次函数的一般形式利用待定系数法确定二次函数的解析式即可;
(2)设P(m,-m2+2m+8),作PH⊥x轴,交x轴于点H,从而得到△EOC∽△EHP,利用相似三角形对应边的比相等得到PH=4OC,从而列出方程-m2+2m+8=4×2,求得m的值即可确定点的坐标;
(3)作PK⊥y轴,从而得到PK=2,KC=8-2=6,然后由翻折得△CQG≌△CQP,从而得到QG=QP,CG=CP=2
,然后在Rt△OCG中求得GO的长即可求得点G的坐标.
(2)设P(m,-m2+2m+8),作PH⊥x轴,交x轴于点H,从而得到△EOC∽△EHP,利用相似三角形对应边的比相等得到PH=4OC,从而列出方程-m2+2m+8=4×2,求得m的值即可确定点的坐标;
(3)作PK⊥y轴,从而得到PK=2,KC=8-2=6,然后由翻折得△CQG≌△CQP,从而得到QG=QP,CG=CP=2
| 10 |
解答:解:(1)∵y=x+2,
∴A(-2,0),
∵D的纵坐标为5,
∴5=x+2,
解得:x=3
∴D(3,5),
又∵A(-2,0)D(3,5)在抛物线y=-x2+bx+c上,
∴
解得
∴抛物线的解析式为y=-x2+2x+8;
(2)设P(m,-m2+2m+8),
作PH⊥x轴,交x轴于点H,
∴CO∥PH,
∴△EOC∽△EHP,
∴
=
,
∵PC=3CE,
∴
=
=
,
∴PH=4OC,
∴-m2+2m+8=4×2,
解得 m=2,或m=0(舍去),
∴P(2,8);
(3)作PK⊥y轴,
∴PK=2,KC=8-2=6,
在Rt△CPK中,CP=2
,
由翻折得△CQG≌△CQP,
∴QG=QP,CG=CP=2
,
在Rt△OCG中,
∵CP=2
,OC=2,
∴GO=6,
∴G(6,0)或G(-6,0),
过P作PH⊥x轴,则H(2,0),且PH=8,
设Q(n,0)
则QP2=PH2+QH2=82+(n-2)2,
GQ=|xQ-xG|=|n-(±6)|
因为QG=QP,
82+(n-2)2=[n-(±6)]2,
解得n=-4,或n=2,
∴Q(-4,0)或Q(2,0).
∴A(-2,0),
∵D的纵坐标为5,
∴5=x+2,
解得:x=3
∴D(3,5),
又∵A(-2,0)D(3,5)在抛物线y=-x2+bx+c上,
∴
|
解得
|
∴抛物线的解析式为y=-x2+2x+8;
(2)设P(m,-m2+2m+8),
作PH⊥x轴,交x轴于点H,

∴CO∥PH,
∴△EOC∽△EHP,
∴
| EC |
| EP |
| CO |
| PH |
∵PC=3CE,
∴
| EC |
| EP |
| CO |
| PH |
| 1 |
| 4 |
∴PH=4OC,
∴-m2+2m+8=4×2,
解得 m=2,或m=0(舍去),
∴P(2,8);
(3)作PK⊥y轴,
∴PK=2,KC=8-2=6,

在Rt△CPK中,CP=2
| 10 |
由翻折得△CQG≌△CQP,
∴QG=QP,CG=CP=2
| 10 |
在Rt△OCG中,
∵CP=2
| 10 |
∴GO=6,
∴G(6,0)或G(-6,0),
过P作PH⊥x轴,则H(2,0),且PH=8,
设Q(n,0)

则QP2=PH2+QH2=82+(n-2)2,
GQ=|xQ-xG|=|n-(±6)|
因为QG=QP,
82+(n-2)2=[n-(±6)]2,
解得n=-4,或n=2,
∴Q(-4,0)或Q(2,0).
点评:本题是二次函数的综合题型,其中涉及到的知识点有待定系数法确定二次函数的解析式.在求有关动点问题时要注意分析题意分情况讨论结果.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
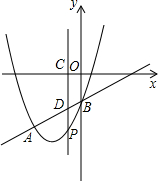 如图,抛物线y=x2+bx+c与直线y=x-1交于A、B两点.点A的横坐标为-3,点B在y轴上,点P是y轴左侧抛物线上的一动点,横坐标为m,过点P作PC⊥x轴于C,交直线AB于D.
如图,抛物线y=x2+bx+c与直线y=x-1交于A、B两点.点A的横坐标为-3,点B在y轴上,点P是y轴左侧抛物线上的一动点,横坐标为m,过点P作PC⊥x轴于C,交直线AB于D. 如图,已知反比例函数y=
如图,已知反比例函数y=